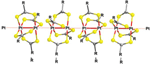Supramolecular Organization of Bimetallic Building Blocks: from Structural Divertimentos to Potential Applications

Received 23 April 2013; Accepted 22 May 2013; Publication 6 June 2013

Journal of Self-Assembly and Molecular Electronics, Vol. 1, 149–176.
doi: 10.13052/jsame2245-4551.121
Copyright © 2013 River Publishers. All rights reserved.

Ruben Mas-Balleste^* and Felix Zamora^*

Departamento de Química Inorgánica, Universidad Autónoma de Madrid, 28049 Madrid, Spain
Corresponding authors: ruben.mas@uam.es; felix.zamora@uam.es

Abstract

The phenomena that results on supramolecular aggregations of bimetallic [Pt₂L₄] and [AuL₂] are reviewed. Supramolecular [AuL₂]_n (n=2,3) were observed in some cases in solution as a result of Au(I)⋯Au(I) aurophilic interactions, which also direct the assembly of oligomeric structures in crystal phase. Analogously, Pt(II)⋯Pt(II) attraction accounts for the assembly of [Pt₂L₄]_nsupramolecules which can result on 1D semiconductive arrangements in crystal phase and direct the formation of 1D nanofibres on surfaces. Finally, oxidation of [Pt₂L₄] to [Pt₂L₄I]_n produces highly conductive polymers that can reversibly assemble/disassemble into [Pt₂L₄] and [Pt₂L₄I₂]. Such outstanding ability results on an unprecedented processability that enables MMX polymers for technological applications as molecular wires.

Keywords

Metal-metal interactions
Supramolecular assemblies
MMX Chains
Molecular wires

1. Introduction

In recent years, considerable attention has been paid to the design and synthesis of molecular materials and devices [1] being the organization of molecules a main goal in both material science and nanoscience. The systematic use of weak interactions to assemble complex structures is the ultimate challenge in supramolecular chemistry.[2] But while hydrogen bonding has been widely studied, other types of intermolecular interactions such as weak metal⋯metal interactions still remain less explored.[3] On the other hand, compounds containing metal-metal interactions is a field that has attracted great attention during years in material science because of their unusual electronic properties, magnetism and/or electrical conductivity.[3b] This “old topic” has gained renewed attention in the preparation and characterization of materials with high anisotropy and restricted dimensionality. The reason is very simple and can be understood taking into account that small pieces of matter may show very unusual optical, magnetic, and conducting properties due to their size once they go into the nanoscale.

Metal-metal interaction is the driving force to form some linear structures with interesting properties. Several reports suggest that weak metal-metal interactions can be used to build up complex structures.[3b] Such attractive interactions are mainly observed between units containing Pt(II), Ag(I) or Au(I) centres. For example, tetracyanoplatinates, K₂Pt(CN)₄X_0.3.nH₂O (X=Cl, Br), named KCPs, were one of the first examples showing electrical conductivity.[4] These systems are formed by the stacking of square-planar [Pt(CN)₄]^n- anion complexes.[5] The structures show the overlapping of 5d_z² orbitals strongly affected by the Pt-Pt intermolecular distances that also affect to their conductive properties. KCP based materials represent the first inorganic “molecular wires” ever designed.[6] Similarly, analogous columnar systems have been formed with dimetallic precursors, for instance [Pt₂(S₂CR)₄] (R= alkyl group).[7] These discrete dinuclear complexes with intermolecular metal-metal interactions have fascinating magnetic and electrical properties.[8] Some of them have been shown to be suitable as precursors for weakly-bound one-dimensional metal chains.[9] But probably one of the most studied metal-metal interactions is the tendency of Au(I) centres to establish weak Au(I)⋯Au(I) bonding, named aurophilia.[10] This phenomenon is a consequence of a combination of dispersion forces and the mixing of filled 5d-based molecular orbitals and empty molecular orbitals of appropriate symmetry derived from the 6s and 6p orbitals.[11] As a consequence of this supramolecular interaction, and taking advantage of the structural versatility of Au(I) centres, a variety of structures with interesting optical and/or electrical properties have been reported.[12, 13]

However, a deeper understanding of the chemical principles that direct such assemblies is still an important challenge in chemistry and could probably has an impact in nanoscience.

The goal of this review is to provide a current overview on the recent studies devoted to bimetallic species containing the basic structural units [Au₂(S₂CR)₂] or [Pt₂(S₂CR)₄] as well as the linear structures resulting from combination of diplatinum units and iodide bridging ligands.

2. Gold(I)⋯gold(I): Golden attraction

2.1. In Crystal Phase

Crystal structures reported for homolepticAu(I)-dithiocarboxylato compounds reveal an outstanding ability to generate oligomeric/polymeric structures by means of the $μ$ -kS:kS’ bridging mode. From such structures a complex series of intra- and inter-molecular supramolecular interactions can be found. Only in the case of [Au₂(isobutyldithiocarboxylato)₂], the existence in the crystalline phase of two polymorphic forms have been reported: one formed by discrete [Au₂L₂] bimetallic units and other formed polymeric [AuL]_n chains. In that case, intermolecular Au⋯Au distance all fall far from the range of significant aurophilic interactions.[14]

The scenario found for xanthato ligands differs substantially from what is observed for dithiocarboxylato containing compounds. All structures known consist on discrete dimeric entities in which the metal centres are joined by double $μ$ -kS:kS’xanthate bridges leading to essentially planar eight-member Au₂S₄C₂ rings. While strong intramolecular aurophilic interaction between the gold(I) centres is generally observed, not allways significant intermolecular interactions are found. Only in the case of [Au₂(isopropyl-xanthate)₂] Au⋯Au at around of 3.0 Å have been observed indicating aurophilic attractive intermolecular interactions.

The preponderance of double bridged dimers observed for xanthato ligands is also found for dithiocarbamate containing Au(I) compounds. However, dithiocarbamate containing [Au₂L₂] structures tend to establish short Au⋯Au intermolecular distances. For the case of the dithiocarbamate, there is one ligand that provides both single-bridge-based (oligomeric) structures and double bridged dimers. However, in that case, only a severe increase of the concentration of gold in the reaction media, allows to overcome the appearance of the more favourable dimeric-based crystal structure.

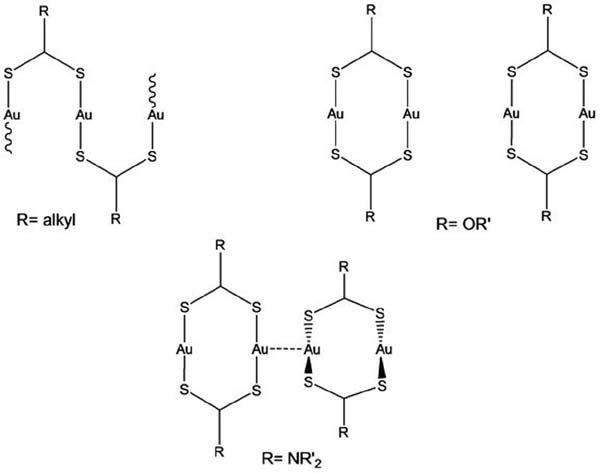
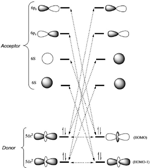
Overall, as shown in Figure 1 regarding the nuclearity of crystallographically characterized [Au₂L₂] compounds, it appears that there is a higher tendency of the dithiocarboxylato ligands to provide single-bridge-based structures (rings and chains) than in the case of xanthate and dithiocarbamate ligands, where double bridged dimers are preponderant. While xanthates prefer do not establish intermolecular aurophilic interactions, dithiocarbamate containing complexes follow the opposite trend.

Figure 1 Preferred structural motifs for homoleptic Au(I) compounds containing dithiocarboxylato, xanthato or dithiocarbamato ligands.

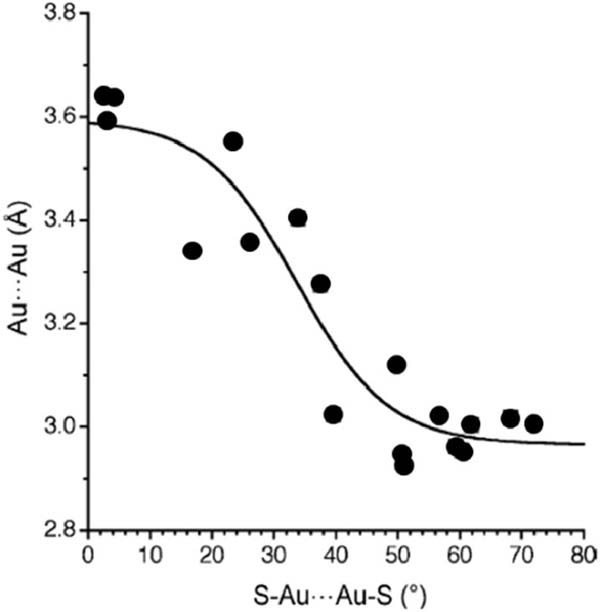
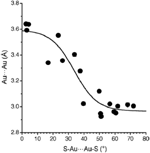
Supramolecular arrangements based on [Au₂L₂] units can mainly be attributed to an Au⋯Au attraction known as aurophilia. While the most stabilizing intermolecular interaction is generally that between two gold atoms, also Au⋯S and S⋯S interactions have been described as driving forces for such assemblies.[14-15] Typically, when the Au⋯Au is found at around 3Å the intermolecular interaction between Au(I) centres is maximized. Interestingly, the Au⋯S interactions are also stabilizing but at somewhat longer distances (with a minimum at around 3.5 Å), whereas S⋯S interactions are destabilizing at short distances and only slightly stabilizing at 3.8–4.0 Å. Analysis of the crystal structures published for [Au₂L₂] units (being L dithiocarboxylates, xanthates, or dithiocarbamates) shows the interplay of the three intermolecular interactions and of their different distance dependence. Regarding the relative orientation of the dinuclear [Au₂L₂], has been found that Au⋯Au distances shorter than 3.30Å are only compatible with a rotated structures, i.e. with S-Au⋯Au-S torsion angles larger than 30º. In contrast, coplanar orientations are only compatible with Au⋯Au distances larger than 3.5 Å. This effect can be clearly appreciated in Figure 2, where a representation of the interdimer Au⋯Au distances (from a CSD search for compounds [Au₂L₂], L=₂SC-X-R, X= C,N,O) as a function of the S-Au⋯Au-S torsion angle is shown.

Figure 2 Dependence of the intermolecular Au⋯Au distances on the S-Au⋯Au-S torsion angle.

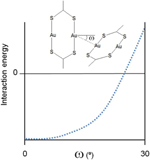
In addition, another geometrical parameter that serves to evaluate the total interaction energy is the relative orientation of the interacting AuS₂ coordination moieties, defined by the Au-Au⋯Au angles ( $ω$ ). An analysis of all short contacts between those units in the CSD shows that the Au⋯Au distances are all longer than 3.88 Å when a gold is found at a $ω$ angle higher than 30º, suggesting that the interaction energy is most stabilizing at the perpendicular orientation.

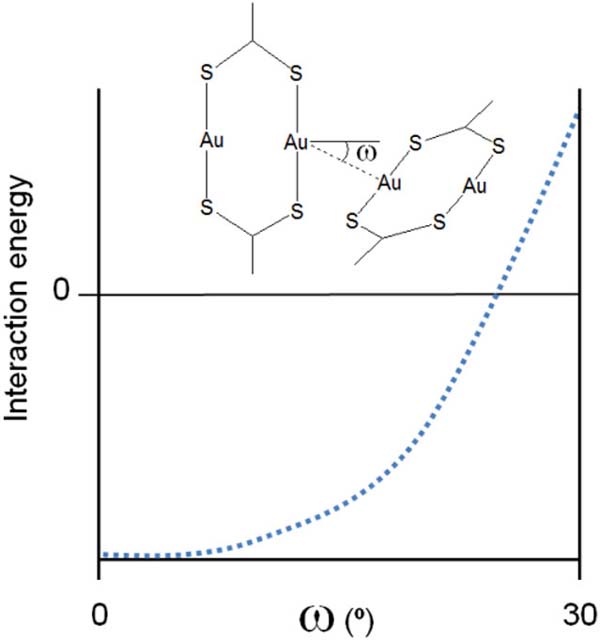
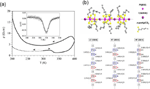
In general, DFT performs poorly at describing accurately the energetics of Au(I)⋯Au(I) interactions. Thus, in order to rationalize the variety of structural patterns found for the supramolecular arrangement of the di- and oligonuclear Au(I) species, computational studies were carried out at the MP2 level of theory, capable of reasonably evaluating the relevant intermolecular interactions. Angular dependence of the strength of the aurophilic interaction was confirmed by BSSE-corrected interaction energy calculations between two dinuclear molecules at a fixed intermolecular Au⋯Au distance of 3.0Å and varying Au-Au⋯Au angles ( $ω$ ). Theoretical results show that the interaction energy varies little for deviations of less than 10º from a perpendicular arrangement, but become much less stabilizing at larger angles (Figure 3).

Figure 3 Theoretically computed dependence on the Au-Au⋯Au angles of the interaction energy between two [Au₂L₂] units.

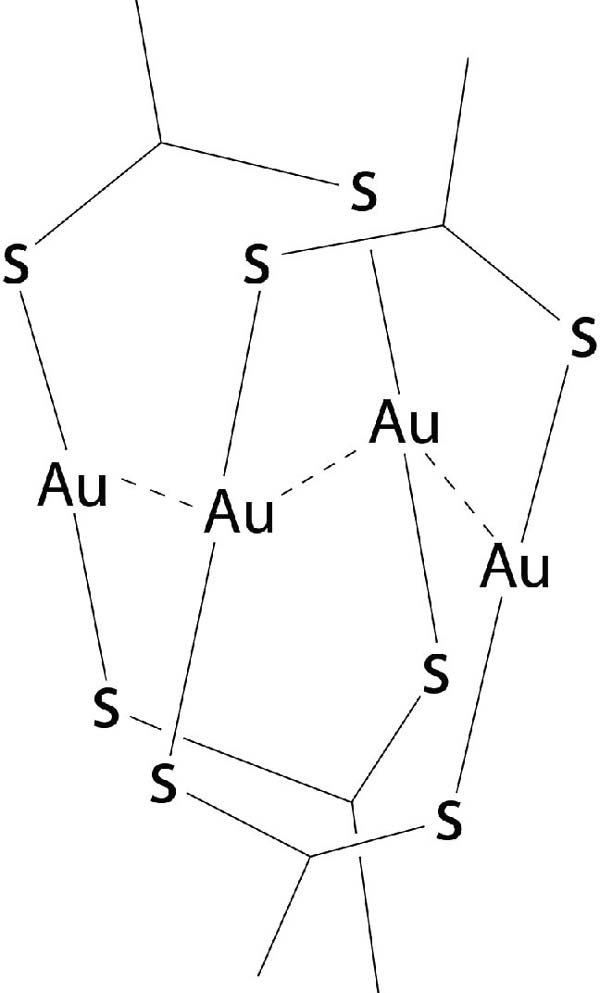
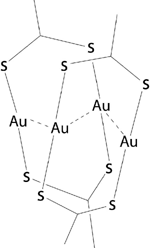
Optimization of the structures [Au₂L₂]₂ (being L dithiocarboxylato or xanthato ligands, see Figure 4), illustrated these concepts. The most stable geometries with each ligand, present structures with stacked Au₂S₄C₂ rings, shifted along the Au-Au direction to form Au4 rhombuses, and also rotated relative to each other. Such arrangement facilitates the existence of three intermolecular Au⋯Au contacts at distances of around 3.0 Å and four Au⋯S contacts at 3.5 Å or shorter, whereas avoiding S⋯S short contacts.

Figure 4 More stable configuration of the [AuL₂]₂ structure, theoretically optimized.

2.2. In Solution

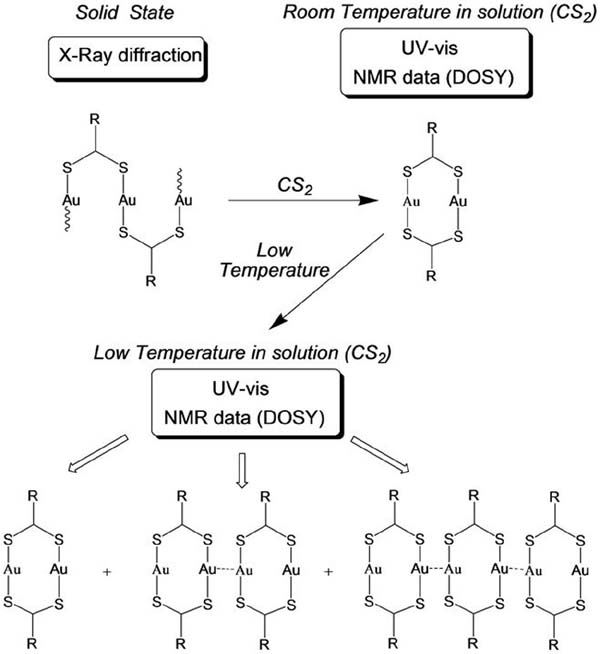
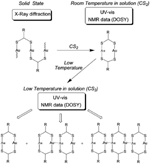
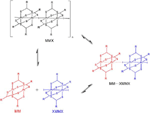
An intriguing feature of [Au₂L₂] (L= dithiocarboxylato) is that for a series of compounds for which different crystal structures have been found, an identical behaviour in solution (in CS₂) has been observed. In fact, the polymeric/oligomeric [Au₂L₂]_n structures found in the crystal phase are cleaved to form discrete analogous [Au₂L₂] entities. Furthermore, spontaneous self-assembly that depends on the temperature and the concentration of the gold compound has been observed for such compounds. Variable temperature UV-vis data shows that lowering the temperature triggers the formation of a new feature at slightly lower energies with respect to that observed at room temperature. This observation was assigned to an aggregation process which reversed upon heating. The appearance of different species in the solutions of [Au₂L₂] (L=dithiocarboxylato) by lowering the temperature was also observed by ¹H NMR spectroscopy. The assessment of the degree of association in solution was obtained by measuring diffusion coefficients (D) from DOSY spectra of a solution at 240 K. According to the measured diffusion coefficient values, the species with a higher hydrodynamic radius (i.e., lower D) become more favourable at lower temperatures. The values obtained in all cases were consistent with the presence of a dimetallic, a tetrametallic, and a hexametallic species [Au₂L₂]_n (n=1, 2, 3) (Figure 5).

Figure 5 Behaviour in solution observed when [Au₂L₂]n (L= dithiocarboxilato) are dissolved in CS₂.

A similar study was performed for analogous Au(I)-xantate compounds. Surprisingly, under the same reaction conditions, for compounds with xanthate ligands no spectroscopic changes (UV-vis and NMR) were found upon decreasing the temperature. Thus, although dithiocarboxylate-containing compounds spontaneously aggregate in solution, analogous complexes with xanthate ligands do not show such behaviour. Different behaviour in solution of [Au₂L₂] depending if L is dithiocarboxylato or xanthato constitutes a case of subtle modulation of the supramolecular interactions between compounds containing Au(I) centres. Considering that steric congestion is equivalent for analogous dithiocarboxylato and xanthato ligands, the tuning of aurophilic assembly should rely on electronic effects. The different behaviour of [Au₂L₂] compounds has been attributed to the different electron-donor or electron-withdrawing nature of L ligands. For the case dithiocarboxylato containing compounds, both oligomeric/polymeric structures and the discrete dimeric ones are generated from the corresponding discrete dimeric [Au₂L₂] entities present in solution. Thus, it is reasonable to assume that the formation of the oligomeric/polymeric [Au₂L₂]_n structures take place through a previous intermolecular aggregation stage of the dimers mediated by the intermolecular aurophilic contacts. Thus, when aggregation in solution is observed (for the dithiocarboxylato compounds) high nuclearities have been found in the crystal phase.

3. Platinum(II)⋯Platinum(II): Platinum Weddings

3.1. In Crystal Phase

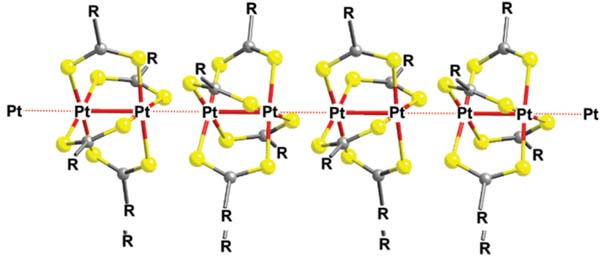
All the reported crystal structures for compounds of the formula [Pt₂L₄] (L=S₂CR) show linear arrangements that are directed by intermolecular Pt(II)⋯Pt(II) interactions. There is only one exception to this tendency for a polymorph reported of [Pt₂(S₂CCH₃)₄], which does not show short Pt⋯Pt distances. Typically, the crystal structures of such compounds consist of quasi-one-dimensional chains based on collinear alignment of [Pt₂(S₂CR)₄] dinuclear entities with short intra- and interdimeric Pt–Pt distances (Figure 6). The dinuclear entities show a windmill-shaped arrangement in which four $μ$ -dithiocarboxylato-kS:kS’ ligands bridge two Pt(II) centres. The [Pt₂L₄] complexes are stacked collinearly along the intradinuclear Pt-Pt axis by means of short interdimer Pt⋯Pt distances (3.0–3.4Å). The steric hindrance of the substituents of the dithiocarboxylato ligands influences the interdimeric Pt⋯Pt distances: the bulkier is the substituent, the longer is the interdimer Pt⋯Pt distance. This effect is reflected on the electrical properties measured on single crystals. Typically, the conductivity measured in single crystals is the characteristic of semiconducting materials and exhibits a remarkable dependence on the intermolecular metal-to-metal distances, being observed that short intermolecular Pt⋯Pt distances enhance conductivity.[9b], [16]

Figure 6 Supramolecular 1D arrangement typically observed in crystalline samples of [Pt₂L₄] compounds.

In principle, analogously to what is observed for Au(I) compounds, one would expect some kind of attraction between Pt and S atoms of adjacent monomers. However, theoretical calculations, indicate that intermolecular S⋯S interaction is of repulsive character in [Pt₂L₄]. As a consequence of such repulsive interactions the energetic minimum adopts a structure with a staggered conformation with dihedral angle S-Pt⋯Pt-S values close to 45º in both crystallographic and calculated structures. These observations, emphasize that the stability of [Pt₂L₄]_n supramolecular entities is due to persistent weak intermolecular metal⋯metal interactions, which are in general difficult to describe by standard DFT methods. In addition, according to theoretical calculations, relativistic and electronic correlation effects are thought to be important in the stability of such aggregates. Thus, to describe accurately the energetics of [Pt₂L₄] dimerisation and predict Pt⋯Pt bond lengths comparable with the available crystallographic experimental data, it is necessary to use a complete basis set and exchange-correlation DFT functionals. Thus, the widely used exchange-correlation functionals BLYP and B3LYP predict a repulsive Pt⋯Pt interaction, a situation that even the long-range corrected functional CAM-B3LYP is not able to correct. After extensive testing, was found that the PBE functional family (which includes its hybrid version PBE0) in the complete basis set limit, provides an optimal compromise between accuracy and computing time.

Theoretical analysis of the charge distribution in [Pt₂L₄]₂ highlighted the leading role of the ligands L in the assembly of [Pt₂L₄]_n through Pt⋯Pt interactions. Specifically, Natural Population Analysis shows the ability of the sulphur atoms to accommodate a part of the charge donated by the platinum atoms resulting in a synergic effect in the stable linear structures.

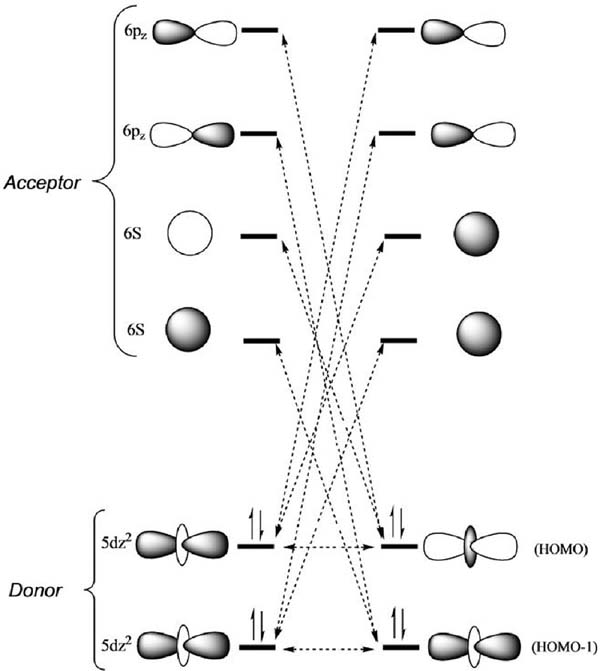
A first approach to understand the electronic description of the Pt⋯Pt bonding between monomer species, can be attempted by computing the change in the energy and the shape of the occupied orbitals depending on the Pt⋯Pt distance. The major changes are observed at the HOMO and HOMO-1 levels, which are degenerated up to 6 Å. Further decrease of the intermolecular distance induces an energy splitting of these MOs. In fact, the HOMO becomes an antibonding combination of mainly 5dz² character with significant contributions of the 6pz and 6s orbitals of Pt and its energy increases upon dimer formation. In contrast, the HOMO-1 is of bonding nature and becomes stabilized upon dimerisation. From this description it is not inferred a neat stabilization, and thus is concluded that the combination of adjacent occupied Pt 5dz² orbitals alone is not sufficient to explain the attractive interactions between Pt(II) centres. Thus, Pt(II)⋯Pt(II) attraction should be explained according to more subtle interactions. The current understanding of the driving force of such weak metal-metal interaction involves a symmetry-allowed mixing between atomic orbitals of adjacent Pt atoms along the Pt-Pt vector namely, the occupied (donor) 5dz² and the empty (acceptor) 6pz and 6s orbitals. Such donor-acceptor interaction is represented in terms of atomic orbitals in Figure 7.[17]

Figure 7 Orbital interactions that account for Pt(II)⋯Pt(II) supramolecular assembly.

3.2. In Solution

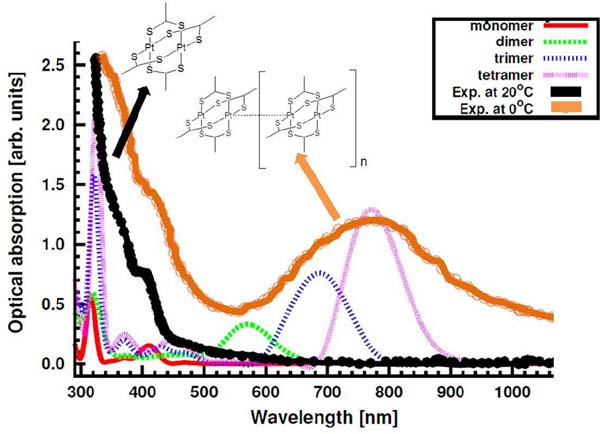
Similarly to what is observed for Au(I), compounds [Pt₂L₄] present a thermochromic behaviour, which depends on concentration, temperature, solvent and nature of ligand. Generally, by decreasing the temperature, a new broad band appears in the red/near-infrared region. This new spectroscopic feature is a very wide band that disappears upon heating and re-appears when the solution is cooled down again. The dependence upon the concentration of such absorbance indicates that it is due to reversible aggregation processes in solution. Determination of the degree of aggregation is in this case more controversial than for Au(I) compounds. A first proposal for aggregation of complex [Pt₂(S₂C(CH₂)₅CH₃)₄] was an equilibrium between the species [Pt₂L₄] and [Pt₂L₄]₂. However, higher nuclearities cannot be discarded.[18] In this case NMR data have not provided a definite answer. Variable-temperature (VT)-¹H NMR measurements did not allowed to distinguish signals from different oligomers. Thus, hints on the nature of supramolecular aggregates should be obtained from a detailed observation of electronic spectroscopy. For the case of complex [Pt₂(S₂C(CH₂)₄CH₃)₄], which presents a good solubility even at low temperatures, several observations indicate that a mixture of different nuclearities can be found in solution at low temperature.

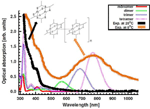
A further support for the assignments of UV-vis spectra at low temperature was obtained from theoretical investigations of the spectroscopic properties of isolated [Pt₂L₄]_n (n=1–4) species (Figure 8). The calculated most intense absorption peaks for the different [Pt₂L₄]_n species are found at approximately $λ$ =410, 570, 686 and 770nm for the series n=1–4. These peaks correspond to neutral excitations from the HOMO (mostly an $σ$ * combination of the Pt 5dz² orbitals) to unoccupied orbitals of s character involving the sulphur ligands. The theoretical simulation of spectra of [Pt₂L₄]_n (n=1–4) clearly indicate that increasing the length of the oligomer results in a decrease of the energy of the optical transition associated to Pt⋯Pt aggregations. Comparison of the experimental and computed spectra clearly suggests that at room temperature only monomeric [Pt₂L₄] species are present, whereas at low temperature a mixture of [Pt₂L₄]_n species with different nuclearities coexists. Furthermore, these calculations show that the position of the band peak in the visible region is very sensitive to the intermolecular Pt⋯Pt distance, which could partially contribute to the broadening of this band.[17]

Figure 8 Experimental UV-vis spectra of [Pt₂(S₂CH₃)₄] at 20ºC or 0ºC in CH₂Cl₂, together with the calculated spectra for [Pt₂(S₂CH₃)₄]_n (n=1–4).

Supramolecular assembly of compounds [Pt₂L₄] can be affected by subtle parameters such as the nature of the ligand L or the solvent in which is dissolved the diplatinum compound. Under the same conditions, there is an evident effect of the ligand that can be related to the steric hindrance that each dithiocarboxylato ligand present in solution. Thus, for L = CH₃-CS₂^-, association is easier than with any other diplatinum complex. When the ligand contains a branched R group the approaching of the dimetal units is definitively more difficult than for compounds that contain linear R groups. Even small differences on the length of linear R chains can have an impact on supramolecular assembly of [Pt₂L₄], being favoured when the R group is a shorter chain. However, crystal structures of [Pt₂(S₂C(CH₂)_nCH₃)₄] (n= 0, 3 and 4) show similar intermolecular Pt⋯Pt distances. Thus, the effective bulkiness of the dithiocarboxylato ligand is not the same in solution and in crystal phase. In fact, ordered packing minimizes steric repulsive interactions especially where linear alkyl chains are present in the structure. However, free motion of such chains in solution provokes significant hindrance, which increases with the length of the alkyl group. This concept is less applicable to branched chains which present a high steric hindrance in solution that cannot be as well overcome in the ordered packing of the crystalline samples.

The effect of the solvent in self-assembly of compounds [Pt₂L₄] in solution has been examined by comparing their behaviour using CH₂Cl₂, CHCl₃, THF and CS₂ as solvent. Under the same conditions, whereas a certain degree of self-assembly in CH₂Cl₂ and (in less extent) in CHCl₃ is observed, CS₂ and THF hamper the association in solution. This effect could, in principle, be justified considering the known coordinative ability of THF and CS₂, which can result in weak metal-ligand interactions between the solvent molecules and the platinum centres. However more subtle effects should be invoked to explain the different effect of CH₂Cl₂ and CHCl₃, which are probably related to solvation effects.

3.3. From Solution to Surface

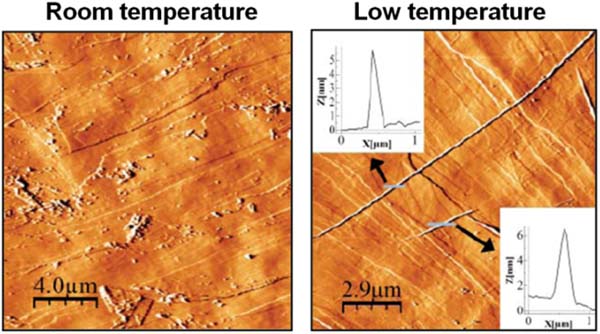
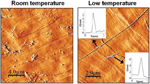
The self-assembly observed in solution at low temperaturetriggered the generation of nanofibers on surfaces (Figure 9). This effect was observed by comparing the results of the adsorption on surfaces of [Pt₂L₄] (L= CH₃-CS₂^-) at low temperature and at room temperature. When a diluted solution of [Pt₂(dta)₄] in CH₂Cl₂ was cooled down to -50ºC and adsorbed, on cooled HOPG surface, AFM images show nanofibers of lengths of up to several microns and heights ranging from 4 to 7nm. However when the same experiment was carried out at room temperature, only amorphous material on HOPG was observed. Interestingly, nanofibers were observed in HOPG but not in mica. Thus, organization of [Pt₂L₄] somehow takes place on the surface, which plays a leading role on the self-assembly process. In particular, as previously observed on related 1D systems, diffusion of small metallic fragments is much easier on HOPG, which can make easier the assembly of nanofibers. Overall, oligomerization of [Pt₂L₄] in a cold solution facilitates the growth of long 1D structures on the surface on an appropriate surface.[9a]

Figure 9 AFM images measured on HOPG surfaces after deposition of solutions of [Pt₂(S₂CH₃)₄] in CH₂Cl₂ at 20ºC and at -50ºC.

4. MMX Chains: Donors and Acceptors with Ephemeral Affairs

4.1. In Crystal Phase

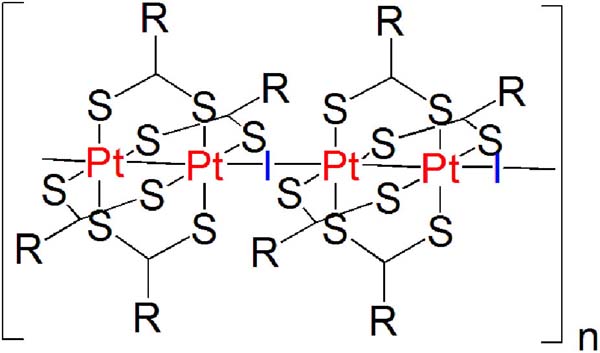
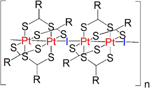
MMX chains belong to the family of mixed-valence metal-organic compounds.[19] Some of these metal-organic polymers show interestingphysical properties.[3] For instance, those based on ruthenium, dicarboxylate and halides, [Ru₂(RCO₂)₄I]_n (R=alkyl group), have shown magnetic properties,[20] and those with platinum, dithiocarboxylate and iodine, [Pt₂(RCS₂)₄I]_n (R=alkyl group), have shown metallic conductivity at room temperature (Figure 10).[21] Monocrystals of [Pt₂(RCS₂)₄I]_n chains have attracted attention in view of their electrical conductivity at room temperature.[21–22]

Figure 10 Representation of a MMX chain based of on platinum, dithiocarboxylate and iodine, [Pt₂(RCS₂)₄I]_n (R=alkyl group).

Another structural feature of [Pt₂(RCS₂)₄I]_n monocrystals is the different types of phase of extreme valence-ordering states that can show depending on the charge states of the metal atoms in the MMX chains [23]: (i) an averaged-valence state (AV): M⁺^2.5 – M⁺^2.5 – X – M⁺^2.5 – M⁺^2.5 – X, (ii) a charge polarization state (CP): M⁺² – M⁺³ – X – M⁺² – M⁺³ – X, (iii) a charge density wave state (CDW): M⁺² – M⁺² – X – M⁺³ – M⁺³ – X, and (iv) an alternate charge polarization state (ACP): M⁺² – M⁺³ – X – M⁺³ – M⁺² – X. The AV and CP states, in which the periodicity of the chain is M-M-X-, are consistent with a metallic and a Mott-Hubbard semiconducting state, respectively. The CDW and ACP states, described as Peierls and spin-Peierls states, are sensitive to structural parameters, and have a doubled M-M-X-M-M-X periodicity unit.

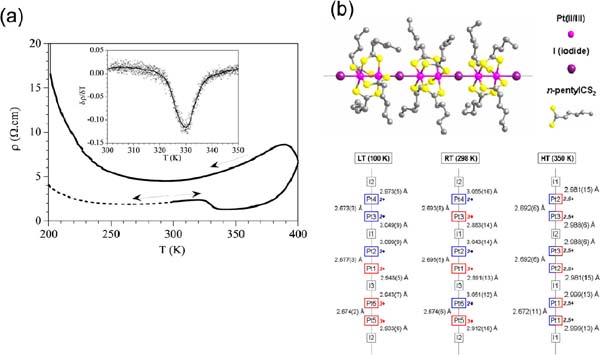
More recently, studies on [Pt₂(RCS₂)₄I]_n (R=alkyl group) chains have shown the high potential of these materials as nano and molecular wires. In a first work, the electrical behaviour of single crystals of [Pt₂(n-pentylCS₂)₄I]_n has been studied. The data have shown conductivity values in the range 0.3–1.4 S.cm^–1 at room temperature.[24] Variable temperature measurements carried out on several crystals following this treatment: (i) heated from 300 to 400 K, (ii) cooled to 100 K, and finally (iii) heating from 100 to 400 K; showed that the first heating scan displayed a metallic behaviour from 300 to 400 K with a transition (RT-HT) that appears as a drop in the resistivity with a negative peak in the derivative at 330 K (Figure 11a). Above this RT-HT transition, the sample recovers its metallic character and reaches a resistivity of ca. 7 $ω$ .cm at 400 K. The transition at 330 K has also been observed in heat capacity measurements, although at a temperature of 324 K, and has been attributed to a moderate disorder of the alkyl chains.[25] When the temperature is decreased from 400 to 100 K, the resistivity smoothly increases to reach a maximum at ca. 390 K (Figure 11a) followed by metallic behaviour from 390 K down to ca. 290 K, where it shows a rounded minimum, similar to that shown by the non-heated crystals, although at a higher temperature. This behaviour confirms the irreversibility of the RT-HT transition. A detailed X-ray diffraction analyses, carried out at different temperatures, confirms the existence of three different phases for [Pt₂(n-pentylCS₂)₄I]_n (Figure 11b). The crystal structures collected at 100 (LT), 298 (RT) and 350 (HT) K confirm that in all cases linear 1D chains generated by repetition of the MMX entities. Each pair of platinum atoms is bridged by four n-pentyl-CS₂ ligands, and the pairs are interconnected by means of linear iodine bridges. The alkyl chain surrounds the Pt-Pt-I-chain precluding the presence of S⋯S contacts. The three-dimensional cohesiveness of the crystal structure is therefore ensured only by means of weak interchain Van der Waals interactions among the alkyl chains. Finally, Density Functional Theory (DFT) calculations allowed the characterization of three different valence-ordering states.

Figure 11 (a) Thermal variation of the electrical resistivity of [Pt₂(n-pentylCS₂)₄I]_n. The dashed line displays the behaviour of a non-heated sample. The inset displays the derivative of the resistivity as a function of the temperature around the RT-HT transition. (b) View of the polymeric [Pt₂(n-pentylCS₂)₄I]_n chain (top) and bond distances distribution along the chain at 100, 298 and 350 K (bottom).

4.2. In Solution

The question about what are the species formed in solution by disolving MMX crystals and what are the experimental factors affecting the MMX chains formation from these solutions, are essential aspects to be solvedin order to understand the chemistry of these molecules and to develop methods to process these materials. The fact that thin films of MMX are almost transparent in thickness, $<$ 50nm, make them extremely appealing for molecular electronics and optoelectronics.

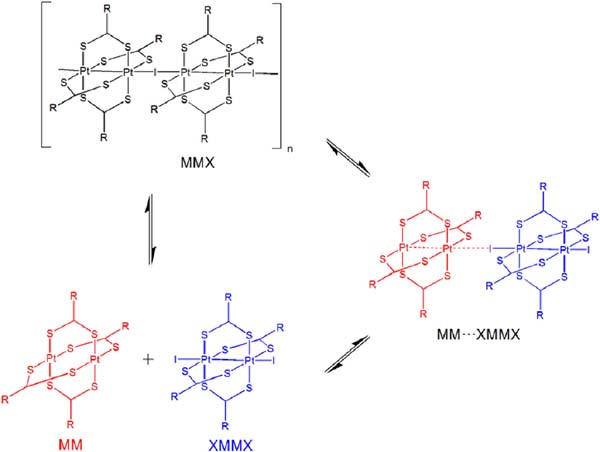
The outstanding ability of the [Pt₂(nBuCS₂)₄I]_n (nBu= n-buthyl) chains to reversibly self-organize from solution is an uncommon behaviour for other metal-organic polymers and raises the questions of which species are present in solution, and which factors have an effect on their subsequent reassembly.[26] In order to address these important factors, the spectroscopic features of [Pt₂(nBuCS₂)₄I]_n dissolved in CH₂Cl₂ were analysed and compared with those of the [Pt₂(nBuCS₂)₄] and [Pt₂(nBuCS₂)₄I₂] precursors. The data showed that, at room temperature, [Pt₂(nBuCS₂)₄I]_n dissociate in solution into an equimolar mixture of [Pt₂(nBuCS₂)₄] and [Pt₂(nBuCS₂)₄I₂]. The\break UV-vis spectrum of a 1mM solution of [Pt₂(nBuCS₂)₄I]_n can be understood as the result of overlapping the UV-vis spectra separately measured from 0.5mM CH₂Cl₂ solutions of precursors [Pt₂(nBuCS₂)₄] and [Pt₂(nBuCS₂)₄I₂]. Consistently, the ¹H NMR spectrum of [Pt₂(nBuCS₂)₄I]_n in CD₂Cl₂ shows an overlapping of the spectra of species [Pt₂(nBuCS₂)₄] and [Pt₂(nBuCS₂)₄I₂]. The spectroscopic data indicate an asymmetric rupture of [Pt₂(nBuCS₂)₄I]_n, which formed two different diamagnetic dimetallic compounds containing two Pt(II) centres (in the case of [Pt₂(nBuCS₂)₄]) or two Pt(III) centres (for [Pt₂(nBuCS₂)₄I₂]) (Figure 12).

Figure 12 Representation of the dissociation and reassembly processes in solution of crystals of [Pt₂(RCS₂)₄I]_n (R=alkyl group) chains.

Concerning the (re)assembly of [Pt₂(nBuCS₂)₄] and [Pt₂(nBuCS₂)₄I₂] in solution, above we have mentioned the ability of the [Pt₂(nBuCS₂)₄] precursor to associate via reversible weak d⁸⋯d⁸ interactions. This can be observed by the appearance at low temperature of an adsorption band at 600–700nm in its UV-vis spectrum. Similar behaviour was observed for solutions of [Pt₂(nBuCS₂)₄I]_n. Additionally, a new band at 820nm appeared in the spectrum of [Pt₂(nBuCS₂)₄I]_n in CH₂Cl₂ at -50ºC. Considering that this feature was not observed for the solutions of pure precursors [Pt₂(nBuCS₂)₄] or [Pt₂(nBuCS₂)₄I₂], this new band indicates the assembly of molecules [Pt₂(nBuCS₂)₄] and [Pt₂(nBuCS₂)₄I₂] generating oligomers of the [Pt₂(nBuCS₂)₄I]_n chains. The ratio between the [Pt₂(nBuCS₂)₄]⋯[Pt₂(nBuCS₂)₄] and the [Pt₂(nBuCS₂)₄]⋯[Pt₂(nBuCS₂)₄I₂] association was affected by the overall concentration of dissolved [Pt₂(nBuCS₂)₄I]_n, being the [Pt₂(nBuCS₂)₄]⋯[Pt₂(nBuCS₂)₄] assembly less favoured at lower concentrations. The low temperature experiments offer valuable insights that help to understand the process of MMX polymer formation from solution.

4.3. From Solution to Surface

Fibres of [Ru₂Br( $μ$ -O₂CEt)₄]_n chains were isolated on different surfaces by casting deposition of water-sodium dodecyl sulphatesolutions.[27] It seems feasible that the evaporation of highly diluted solutions of [Ru₂Br( $μ$ -O₂CEt)₄]_n on the surfaces led to fibre formation. AFM topography images allowed the characterization of homogeneous fibres with lengths from 0.5 to 5mm and typical heights of ca. 0.7nm, corresponding to the isolation on mica of individual polymer chains. The analysis of solutions of [Ru₂Br( $μ$ -O₂CR)₄]_n chains suggested formation of dicationic subunits RuRu⁺ and Br^-. A more detailed study on [Ru₂Br( $μ$ -O₂CEt)₄]_n showed a mechanochemistry based procedure to isolate individual polymer chains on surfaces with sub-nanometer diameter and over microns length. They studied the dynamics process that take place after sonicated solutions of [Ru₂Br( $μ$ -O₂CEt)₄]_n.[28] They demonstrate that ultrasound induces scission of the weaker coordination bonds giving rise to reactive species that self-organize in solution allowing a rich variety of structures. The recognition of these activated building blocks leads to isolate very long individual chains of the MMX polymer when adsorbed on surfaces as demonstrated by the AFM images. It seems that the linear observed structures reproduce those present in the solution. This work suggested a way to form well-organized entities of [Ru₂Br( $μ$ -O₂CR)₄]_n chains on surfaces.

Two different nanostructures were characterized on mica from the controlled deposition of sonicated diluted THF solutions of [Pt₂(n-pentylCS₂)₄I]_n. Using this simple procedure, high density coverage of micron-length fibres of [Pt₂(n-pentylCS₂)₄I]_n with typical height of ca. 1.5 to 2.5nm were isolated. According to the X-ray data (1.5nm being the expected height of one MMX chain), these fibres correspond to a few MMX chains. Additionally, upon increasing the concentration of the initial [Pt₂(n-pentylCS₂)₄I]_n solution, nanocrystals were formed on mica. AFM topographic image of several nanocrystals growing from a central nucleus showed a length of 1–5 $μ$ m and a typical height of 2–4nm (Figure 9).

While formation of structures from solution seems to be a simple and powerful method, at that point the understanding of the parameters controlling both the molecular association in solution and the deposition were unclear.

The rather uncommon feature, dissolution and repolymerization conserving its structural integrity, showed for the [Pt₂(nBuCS₂)₄I]_n chains enables its processability and the formation of organized structures on surfaces. Thus, micromolding in capillaries (MIMIC)[29] and lithographically controlled wetting (LCW)[30] were successfully applied to form a variety of nanostructures (Figure 13).

Figure 13 Topographic AFM images of nanostructures of [Pt₂(n-pentylCS₂)₄I]_n showing over-micron length fibres of ca. 1.5 to 2.5nm of height (a) and flat nanocrystals of 2–4nm height (b).

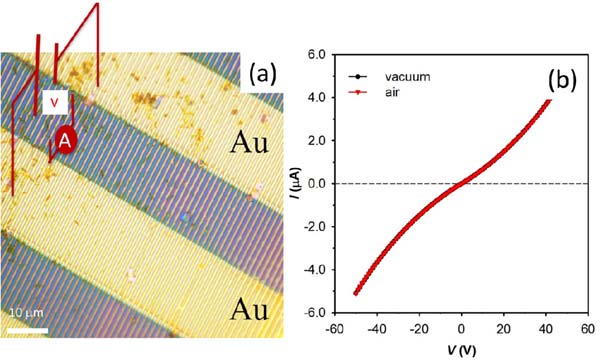
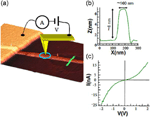
Figure 14 shows an optical micrograph of the interdigitated electrodes of a FET printed by LCW and parallel $μ$ -wires on pre-fabricated gold electrodes that were printed by MIMIC. The electrical characterization performed by measuring the current flowing in the $μ$ -wires as a function of bias voltage, ranging from +50 to -50 V reveals a near Ohmic behaviour. It is important to note that the time stability of the wires is longer than 6 months, in air at room temperature and in high humidity. As an example of direct application of [Pt₂(nBuCS₂)₄I]_n nanostructures, the use of this material as electrodes in organic field-effect transistor (OFET) devices was tested (Figure 15)[31] Thus, structures produced by MIMIC technique on SiO₂/Si from a [Pt₂(nBuCS₂)₄I]_n solution demonstrated that this material can be efficiently used as electrodes for organic field-effect transistor. The OFET devices showed a field-effect performance with charge mobility, $μ$ _sat, up to 5.2×10^-3 cm²V^-1s^-1, with on/off ratios around 10⁶ and an excellent stability under ambient conditions (after six months from fabrication the device remains almost unaltered).

Figure 14 Some microfabricated, by unconventional wet lithography, structures of [Pt₂(nBuCS₂)₄I]_n_. a) Optical micrograph (scale bar=100mm) of interdigitated comb-like electrodes printed on silicon oxide by LCW, b) AFM image and c) SEM image of [Pt₂(nBuCS₂)₄I]_n pattern on silicon oxide.

Figure 15 a) Optical image of parallel $μ$ -wires of [Pt₂(nBuCS₂)₄I]_n printed on silicon oxide by unconventional wet lithography onto Au electrodes. b) Current vs. voltage characteristics of the [Pt₂(nBuCS₂)₄I]_n wires shown in (a).

4.4. From solid to gas phase to surface assembly

Nanostructures obtained from [Pt₂(n-pentylCS₂)₄I]_nsolutions were not suitable to measure the electrical resistance using a macroscopic gold electrode evaporated with a conventional mask technique.[32] Apparently, the nanostructures formed by drop-casting from the polymer solution, contain some amount of solvent retained on the surface in the adsorption process together with the MMX nanostructures. Under a vacuum during the gold sublimation process, the adsorbed solvent rapidly evaporates generating fractures across the MMX nanostructures and avoiding a proper characterization. Therefore, a less conventional approach based on direct sublimation from synthetized monocrystals of MMX was explored. This method has been successfully applied to the adsorption of [Pt₂(n-butylCS₂)₄I]_n on several surfaces.[33] The procedure consists of (i) sublimation of [Pt₂(n-butylCS₂)₄I]_n crystals in a high vacuum chamber (10^-6 mbar), and then (ii) the landing of the sublimated materialon a substrate ata controlled temperature. The analysis by AFM of the surfaces reveals formation of 1D structures, with lengths of several microns and typical heights around 5 to 10nm when the parameters were properly adjusted. The sublimation method produces straighter fibres with more homogeneous width distributions than drop casting procedures. Additionally, it was reported that the dimensions of the structures obtained by sublimation can be modulated by controlling parameters such as the nature of the surface, the deposition time and the annealing temperature. Thus, it has not only been possible to isolate nanofibres, but also form nanocrystals that have very few defects. The mechanism of the sublimation process is still not well established, however, in analogy to what it is observed in solution, it seems likely that the thermal energy applied to the monocrystals is able to induce the breakage of the weaker coordinative bonds leading to the formation of small entities which are volatile under the experimental conditions to fly and land on the surface. Subsequently, these small entities will diffuse and self-assemble to form the MMX chains. This is the description of a reversible process consequence of the reversibility feature of a typical coordinative bond which is the basic feature of a MMX structure.

More recently, the high potential of MMX chains towards their use as molecular wires has been proved. Thus, nanoribbons of [Pt₂(dta)₄I]_n isolated on mica [34] and SiO₂[35] by direct sublimation from crystals have shown outstanding electrical properties.

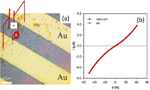
The conductive nanoribbons were formed on mica by direct sublimation from crystals of [Pt₂(dta)₄I]_n under a high vacuum (Figure 16). However, while these nanostructures showed high conductivity the non-linear IV features suggested a significant content of defect in these nanoribbons, therefore limiting their conductivity (Figure 17).[34]

Figure 16 AFM topography image of over micron length nanoribbons formed on mica by direct sublimation of [Pt₂(dta)₄I]_n monocrystals (a). A zoomed nanoribbon (b) and its height profile (c)

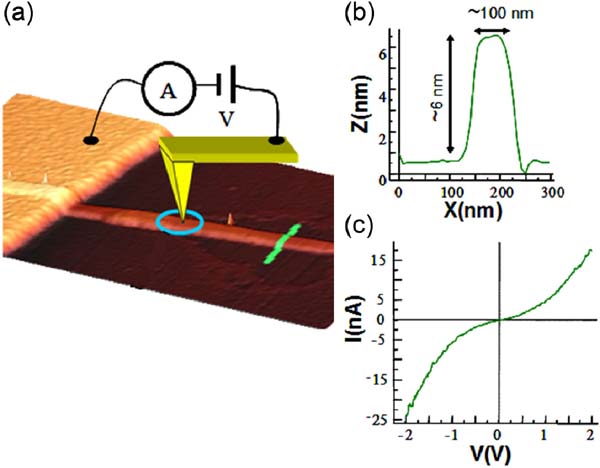
Figure 17 (a) AFM topography showing a MMX nanoribbon adsorbed on mica and connected to a gold electrode. The nanoribbon is partially covered with gold macro-electrode. (b) AFM height profile taken along the green line drawn in (a). (c) Current vs. voltage features taken by contacting the nanoribbon with a gold AFM tip located at 100nm from the gold macro-electrode.

Recently, following a similar experimental procedure to that previously used on mica, [Pt₂(dta)₄I]_n nanoribbons have been isolated on SiO₂. Those nanoribbons are larger but more important they have shown high order, defect-free for distances below ca. 300nm.[35] The conductivity for these nanostructures is 10⁴ S/m, three orders of magnitude higher than that of our macroscopic crystals. This magnitude is preserved for distances as large as 300nm. Above this length, the presence of structural defects (~0.5 \%) gives rise to an inter-fibre mediated charge transport similar to that of macroscopic crystals. Additional experiments show the first direct experimental evidence of the gapless electronic structure theoretically predicted [36] for [Pt₂(dta)₄I]_n chains.

5. Conclusions

According the bibliographic information presented in this review metal⋯metal interactions, Au(I)⋯Au(I) and Pt(II)⋯Pt(II), are the source of spontaneous self-assembly processes. In solution, reversible aggregation of tetra-, hexa- and octa-metallic supramolecules has been observed at low temperatures. These aggregations have different consequences in the solid state structures. For Au(I) containing structures, Au⋯Au interactions trigger oligomerization to generate oligomeric/polymeric [Au₂L₂]_n (L=dithiocarboxylato) structures by means of the $μ$ -kS:kS’ bridging mode. In contrast, Pt(II) compounds show linear arrangements hold together exclusively through Pt⋯Pt interactions. Crystals of [Pt₂L₄] show electrical behaviour characteristic of semiconductors. In addition, supramolecular Pt⋯Pt assembly triggers formation of 1D nanostructures on surfaces. Furthermore, partial oxidation of [Pt₂L₄] with iodine generates supramolecular 1D assemblies of formula [Pt₂L₄I]_n based on week metal-ligand interactions. Assembly and disassembly of [Pt₂L₄I]_n conductive structures, even at the nanoscale, allows to envisage future technological applications in molecular electronics.

References

[1] E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem. Int. Ed., 46, 72–191 (2007).

[2] J. M. Lehn, Proc. Nat. Acad. Sci. USA, 99, 4763–4768 (2002).

[3] a) J. K. Bera and K. R. Dunbar, Angew. Chem. Int. Ed., 41, 4453–4458 (2002); b) F. A. Cotton, C. A. Murillo and R. A. Walton, Multiple Bonds Between Metal Atoms, Springer Science and Business Media Inc., New York (2005).

[4] S. Roth, One-dimensional Metals, VCH, New York (1995).

[5] M.Williams, Adv. Inorg. Chem. Radiochem., 26, 235–268 (1983).

[6] a) R. Mas-Balleste, J. Gomez-Herrero and F. Zamora, Chem. Soc. Rev., 39, 4220–4233 (2010); b) J. Gomez-Herrero and F. Zamora, Adv. Mater., 23, 5311–5317 (2011).

[7] F. A. Cotton, C. Lin and C. A. Murillo, Acc. Chem. Res., 34, 759–771 (2001).

[8] F. A. Cotton and R. A. Walton, Multiple Bonds Between Metal Atoms, 2nd ed., Clarendon, Oxford (1993).

[9] a) R. Mas-Balleste, R. Gonzalez-Prieto, A. Guijarro, M. A. Fernandez-Vindel and F. Zamora, Dalton Trans., 7341–7343 (2009); b) A. Guijarro, O. Castillo, A. Calzolari, P. J. S. Miguel, C. J. Gomez-Garcia, R. di Felice and F. Zamora, Inorg. Chem., 47, 9736–9738 (2008); c) A. Kobayashi, T. Kojima, R. Ikeda and H. Kitagawa, Inorg. Chem., 45, 322–327 (2006).

[10] a) H. Schmidbaur and A. Schier, Chem. Soc. Rev., 37, 1931–1951 (2008); b) P. Pyykko, Chem. Soc. Rev., 37, 1967–1997 (2008).

[11] a) A. Vogler and H. Kunkely, Chem. Phys. Lett., 150, 135–137 (1988); b) P. Pyykko andY. F. Zhao, Angew. Chem. Int. Ed., 30, 604–605 (1991); c) Y. Jiang, S. Alvarez and R. Hoffmann, Inorg. Chem., 24, 749–757 (1985); d) P. K. Mehrotra and R. Hoffmann, Inorg. Chem., 17,\break 2187–2189 (1978); e) A. Dedieu and R. Hoffmann, J. Am. Chem. Soc., 100, 2074–2079 (1978); f) K. M. Merz and R. Hoffmann, Inorg. Chem., 27, 2120–2127 (1988); g) M. A. Carvajal, S. Alvarez and J. J. Novoa, Chem. Eur. J., 10, 2117–2132 (2004).

[12] a) V. W. W. Yam and E. C. C. Cheng, Top. Curr. Chem., 281, 269–309; b) R. J. Puddephatt, Coord. Chem. Rev. 2001, 216, 313–332 (2007).

[13] a) V. W. W. Yam and E. C. C. Cheng, Chem. Soc. Rev., 37, 1806- 1813 (2008); b) H. Schmidbaur and A. Schier, Chem. Soc. Rev., 41, 370–412 (2012).

[14] a) M. L. Gallego, A. Guijarro, O. Castillo, T. Parella, R. Mas-Balleste and F. Zamora, Cryst. Eng. Commun., 12, 2332–2334 (2010); b) M. R. Azani, O. Castillo, M. L. Gallego, T. Parella, G. Aullon, O. Crespo, A. Laguna, S. Alvarez, R. Mas-Balleste and F. Zamora, Chem. Eur. J., 18, 9965–9976 (2012).

[15] a) D. D. Heinrich, J. C.Wang and J. P. J. Fackler, Acta Crystall. C, 46, 1444 (1990); b) M.A. Mansour,W.B. Connick, R. J. Lachicotte, H. J. Gysling and R. Eisenberg, J. Am. Chem. Soc., 120, 1329 (1998); c) M. A. Mansour, W. B. Connick, R. J. Lachicotte, H. J. Gysling and R. Eisenberg, J. Am. Chem. Soc., 120, 1329 (1998); d) R. Hesse and P. Jennische, Acta Chem. Scand., 26, 3855 (1972); e) S. Y. Ho and E. R. T. Tiekink, Z. Kristall. New Cryst. Struct., 217, 589 (2002).

[16] a) C. Bellitto, M. Bonamico, G. Dessy, V. Fares and A. Flamini, J. Chem. Soc. Dalton Trans., 35–40 (1987); b) C. Bellitto, G. Dessy, V. Fares and A. Flamini, J. Che. Soc. Chem. Commun., 409–411 (1981).

[17] A. P. Paz, L. A. Espinosa Leal, M. R. Azani, A. Guijarro, P. J. S. Miguel, G. Givaja, O. Castillo, R. Mas-Balleste, F. Zamora and A. Rubio, Chem. Eur. J., 18, 13787–13799 (2012).

[18] T. Kawamura, T. Ogawa, T. Yamabe, H. Masuda and T. Taga, Inorg. Chem., 26, 3547–3550 (1987).

[19] M. Yamashita and H. e. Okamoto, Material Designs and New Physical Properties in MX- and MMX-Chain Compounds, Springer-Verlag Wien (2013).

[20] a) M. C. Barral, R. Gonzalez-Prieto, R. Jimenez-Aparicio, J. L. Priego, M. R. Torres and F. A. Urbanos, Eur. J. Inorg. Chem., 2339–2347 (2003); b) M. C. Barral, R. Gonzalez-Prieto, R. Jimenez-Aparicio, J. L. Priego, M. R. Torres and F. A. Urbanos, Eur. J. Inorg. Chem., 4491–4501 (2004); c) M. C. Barral, R. Jimenez-Aparicio, D. Perez-Quintanilla, J. L. Priego, E. C. Royer, M. R. Torres and F. A. Urbanos, Inorg. Chem., 39, 65–70 (2000).

[21] a) H. Kitagawa, N. Onodera, T. Sonoyama, M. Yamamoto, T. Fukawa, T. Mitani, M. Seto and Y. Maeda, J. Am. Chem. Soc., 121, 10068–10080 (1999); b) M. Mitsumi, T. Murase, H. Kishida, T. Yoshinari, Y. Ozawa, K. Toriumi, T. Sonoyama, H. Kitagawa and T. Mitani, J. Am. Chem. Soc., 123, 11179–11192 (2001).

[22] M. Mitsumi, K. Kitamura, A. Morinaga, Y. Ozawa, M. Kobayashi, K. Toriumi,Y. Iso, H. Kitagawa and T. Mitani, Angew. Chem. Int. Ed., 41, 2767–2771 (2002).

[23] Y. Wakabayashi, A. Kobayashi, H. Sawa, H. Ohsumi, N. Ikeda and H. Kitagawa, Journal of the American Chemical Society, 128, 6676–6682 (2006).

[24] A. Guijarro, O. Castillo, L. Welte, A. Calzolari, P. J. S. Miguel, C. J. Gomez-Garcia, D. Olea, R. di Felice, J. Gomez-Herrero and F. Zamora, Adv. Funct. Mater., 20, 1451–1457 (2010).

[25] K. Saito, S. Ikeuchi, Y. Nakazawa, A. Sato, M. Mitsumi, T. Yamashita, K. Toriumi and M. Sorai, J. Phys. Chem. B, 109, 2956–2961 (2005).

[26] D. Gentili, G. Givaja, R. Mas-Balleste, M. R. Azani, A. Shehu, F. Leonardi, E. Mateo-Marti, P. Greco, F. Zamora and M. Cavallini, Chem. Sci., 3, 2047–2051 (2012).

[27] D. Olea, R. Gonzalez-Prieto, J. L. Priego, M. C. Barral, P. J. de Pablo, M. R. Torres, J. Gomez-Herrero, R. Jimenez-Aparicio and F. Zamora, Chem. Commun., 1591–1593 (2007).

[28] L. Welte, R. González-Prieto, D. Olea, M. Rosario Torres, J. L. Priego, R. Jiménez-Aparicio, J. Gómez-Herrero and F. Zamora, ACS Nano, 2, 2051–2056 (2008).

[29] a) E. Kim, Y. N. Xia and G. M. Whitesides, Nature, 376, 581–584 (1995);b) M. Cavallini, C. Albonetti and F. Biscarini, Adv. Mater., 21, 1043–1053 (2009).

[30] a) M. Cavallini and F. Biscarini, Nano Letters, 3, 1269–1271 (2003);b) M. Cavallini, D. Gentili, P. Greco, F. Valle and F. Biscarini, Nat. Prot., 7, 1668–1676 (2012).

[31] H. B. Akkerman, P.W. M. Blom, D. M. de Leeuw and B. de Boer, Nature, 441, 69–72 (2006).

[32] P. J. de Pablo, M. T. Martinez, J. Colchero, J. Gomez-Herrero, W. K. Maser, A. M. Benito, E. Munoz and A. M. Baro, Adv. Mater., 12, 573–576 (2000).

[33] L.Welte, U. García-Couceiro, O. Castillo, D. Olea, C. Polop,A. Guijarro, A. Luque, J. M. Gómez-Rodríguez, J. Gómez-Herrero and F. Zamora, Adv. Mater., 21, 2025–2028 (2009).

[34] L. Welte, A. Calzolari, R. di Felice, F. Zamora and J. Gómez-Herrero, Nat. Nanotech., 5, 110–115 (2010).

[35] C. Hermosa, J. V. Álvarez, M. R. Azani, C. J. Gómez-García, M. Fritz, J. M. Soler, J. Gómez-Herrero, C. Gómez-Navarro and F. Zamora, Nat. Commun., 4, 1709 (2013).

[36] A. Calzolari, S. S. Alexandre, F. Zamora and R. Di Felice, J. Am. Chem. Soc., 130, 5552–5562 (2008).

Biographies

Rubén Mas-Ballesté was born in Barcelona (Catalonia, Spain) in October of 1975. In 2004 he got his Ph.D. under the supervision of Prof. Pilar González-Duarte and Prof. Agustí Lledós at Universitat Autónoma de Barcelona. From June 2004 to November 2007 he was working in the Lawrence Que's group at the University of Minnesota (USA) as a postdoctoral associate. At the present he is an associate professor at the Universidad Autónoma de Madrid (Spain) where he was appointed under the “Ramón y Cajal” program in 2008. His research is focused on activation/formation of small molecules, synthesis and reactivity of 2D organic polymers and inorganic materials for nanotechnology.

Félix Zamora was born in 1967 in Cuenca (Spain). In 1994 he obtained the PhD in Inorganic Chemistry at Universidad Autónoma de Madrid. He moved to University of Dortmund (Germany) to work with Professor B. Lippert. He is currently “Profesor Titular” at the Inorg. Chem. Department at the Universidad Autónoma de Madrid. From 2004 he focused on new nanomaterials based on inorganic systems such as coordination polymers.