Interaction of DNA Bases with Gold Substrates
Received 6 December 2012; Accepted 17 December 2012
Journal of Self-Assembly and Molecular Electronics, Vol. 1, 41–68.
doi: 10.13052/same2245-4551.112
Copyright © 2013 River Publishers. All rights reserved.
Marta Rosa*, Wenming Sun*, Rosa Di Felice*
- Center S3, CNR Institute of Nanoscience, Via Campi 213/A, 41125 Modena, Italy
- *Corresponding author: rosa.difelice@unimore.it
Abstract
The interaction of molecules with inorganic substrates is a crucial issue for applications in molecular electronics. It influences important factors such as the immobilization efficiency and the charge injection through the interface. Moreover, mechanical aspects connected to the unfolding of biological molecules are important.
We hereby present recent efforts in our group to tackle these problems, based on density functional theory calculations. In particular, we discuss our results on the adsorption of cytosine on Au(111) and on the interaction of guanine, in its natural and size-expanded forms, with small Au clusters. We find that cytosine binds to the Au(111) surface with a mechanism that involves charge sharing, intermediate between chemisorption and physisorption. The investigation of small complexes between guanine and gold clusters reveals the formation of hydrogen bonds: these configurations with unusual bonds are relevant at the corners of nanoparticles, while they can probably be neglected when DNA binds on flat extended metal surfaces.
Keywords
- DNA/Au interfaces
- Density Functional Theory
- Van der Waals
- DNA modifications
- electronic hybridization
1. Introduction
The electronic structure of DNA molecules started to attract the attention of scientific research groups because of its implications in DNA damage and repair. Prompted by encouraging results from measurements of fast charge transfer in ensembles of DNA molecules in solution, scientists later started to query the possibility to exploit DNA molecules in nanotechnology.
The pioneering experiments on the conductivity of DNA between electrodes were published between 1998 and 2000 [1–4] and showed a variety of electrical behaviors. Since then, much conceptual progress has been made in rationalizing the diverse results [5, 6], by understanding the relevance of surface deposition, electrode contacts, probing single molecules rather than uncontrolled networks and many other factors implied in handling flexible soft biological molecules rather than stiff inorganic (or even organic) materials. For instance, two beautiful experiments were realized in more recent years by avoiding the deposition on a hard substrate and optimizing the electrode-DNA contacts through thiol linkers [7, 8]. Furthermore, new avenues for the exploitation of electrical conductance through DNA have been opened [9].
Our group has intensely worked in the past 10 years on the characterization of the structure and electronic properties of DNA fragments by means of Density Functional Theory (DFT) calculations and Molecular Dynamics (MD) simulations, in close collaboration with experimental groups for interpretation of available data and guidance of new experimental routes (e.g., see our joint exp-theo publications [10–14]). In this short review we focus, instead, on more recent work aimed at addressing the issues of surface deposition and electrode contacts [15, 16]. These issues are closely related to the title of the journal and of the SAME conference that launched the series (“Self-Assembly and Molecular Electronics”, Aalborg, Denmark, October 11–12, 2012).
Before doing so, we briefly summarize the basic concepts that emerge from our studies of natural and modified DNA molecules in the gas phase and in solution. We are interested in modified DNAs because chemical and structural alterations may be an effective way to manipulate the electrical behavior of nucleic acids. We argue that natural double-stranded DNA (dsDNA) does not sustain coherent transport through a band-like mechanism, because the electronic structure does not reveal dispersive bands [13, 17]; yet, the electron states are delocalized through the base stack and this superposition may support a form of charge mobility. Continuous wires made of G4 tetrads have a higher density of states close to the fundamental energy gap and a higher amplitude of the occupied states [18, 19], which makes them more promising than dsDNA for exploitation in nanotechnology [10, 20]. Hybridization of each pair in dsDNA with a metal ion is a tool to modulate the fundamental energy gap between electron states [21]. A particularly appealing chemical modification of DNA consists of inserting a benzene ring coplanar to the heterocycles of each base, to form size-expanded xDNA [22]. We have investigated the ground-state and excited-state electronic structure of this variant [23, 24] and compared the results to natural dsDNA: we find that, consistently with the intuition of enhanced aromaticity due to the benzene cycle, the π-π coupling between stacked bases increases, with consequences on the ability to conduct charges. Our most recent work is devoted to a viable protocol to take into account the structural flexibility in a solution environment in the computation of the electronic structure of DNAs by high-level DFT methods. We have noted, on the stream of other authors [25–28], that a single frozen structure is not enough to determine the electronic properties of DNA to a quantitative precision that is desired to compare with real experimental data: in fact, different structures may give very different results [23, 24] and the fluctuations should be sorted out for an average picture. Therefore, we are now applying a multi-step procedure that consists of: (1) MD simulation of a DNA (or modified DNA) oligomer in explicit solvent for 100–500 ns; (2) DFT or time-dependent DFT (TDDFT) calculations on selected structures from the MD trajectory. Step 1 is preceded by the DFT-based generation of classical force fields in the case of DNA derivatives for which parameters are missing in the existing public libraries. To go from step 1 to step 2, one would in principle like to sample the trajectory at regular time interval, so that the electronic quantities can be eventually averaged in time. Driven by the need for restricting the number of selected structure to a small value, we opt instead for a different route: we sort the trajectory by a clustering method to extract few representative structures. From these structures, which are not regular snapshots at given times, we are not able to compute a time average of the desired quantities (e.g., optical spectra or transfer integrals); yet, we can understand the structural variability and recover an average picture by exploiting the occurrence of each representative structure along the trajectory. This multi-step protocol has been recently applied to the optical properties of triplex DNA [29] and to the transport properties of a modified duplex DNA [30]. We are continuing to apply and validate the methodology on other appealing modified DNAs.
Figure 1 Three-dimensional scheme of a scanning tunneling microscopy experiment on a single DNA molecule. The target molecule lies horizontally on a metal surface: it is still debated whether the double helix remains intact and understanding this issue is a main goal of our research. In other kinds of experiments, thiol linkers are employed to hook DNA to electrodes at the 3’ and 5’ ends: we want to understand the role of the length and chemical nature of the linkers in the charge transfer between the electrodes and the molecule.
The above background is not intended as a comprehensive survey of the field, but as a brief summary of our knowledge and understanding based on our own research experience. A broader viewpoint on the state-of-the-art theoretical/computational knowledge on the electronic structure of DNA in the perspective of nanoelectronics can be gathered from a good recent review [31]. We now turn to the core topics of this article. One peculiar aspect of nanotechnologies with biological molecules is that they are usually manipulated in setups different from the biological environment. The interaction between biomolecules and inorganic surfaces and nanoparticles is of great importance in natural systems and for the design of bio-nano molecular devices. DNA molecules are deposited onto inorganic substrates for imaging experiments, contacted by metallic tips for spectroscopy and transport experiments [6] (Figure 1). What happens at these interfaces is a major factor to determine the conductance of DNA molecules in a non-native environment and to interpret real experiments. Our early steps towards a thorough investigation of these problems are reported in Sections 2 and 3. In Section 4 we draw our conclusions and consider possible developments in the field. We focus our attention on gold as a substrate because, due to its chemical inertness and biocompatibility, it could be utilized in several bio-electronic and bio-medical applications.
2. The Interaction of DNA Bases with a Flat Gold Surface: The Case of Cytosine on Au(111)
2.1. The Strategy
The theoretical investigation of the fate of a DNA molecule on a hard substrate, such as in the conditions for scanning tunneling microscopy (STM, Figure 1) or atomic force microscopy (AFM) in their various implementations, is not an easy task. One recurring question that still remains unanswered is whether the double helix unfolds. No single computational technique is suitable to accurately deal with all the different length and time scales of the problem.
On the one hand, it is important to take into account the interaction of each DNA base with the surface at the quantum level, because the critical balance of base-base and base-substrate interactions will determine the preference for folded molecule versus a situation in which the nucleotides can interact more strongly with the host substrate: this length scale can be tackled by means of Density Functional Theory to determine geometry variations in the base and in the substrate upon adsorption, the behavior of the electrons with possible charge transfers and the accurate energetics. On the other hand, unfolding is a process that involves large objects and long times, which are not accessible by ab initio electronic structure methods.
To gain fundamental insights into the problem of DNA/surface coupling, we adopted a multi-step approach that was recently proposed for proteins on surfaces [32], based on the combination of DFT calculations, MD simulations and docking simulations. Thanks to the energetic and structural results obtained with DFT calculations of individual bases on a surface of choice, it is possible to develop a classical force field for atomistic MD simulations of an entire DNA oligomer on the surface. While reliable classical force fields are available for nucleic acids and inorganic materials separately, parameters to describe the interaction have not been developed to date. The DFT results are not only instrumental to force field development, but bring insights into the specific system: in particular, they allow us to unravel the mechanisms of adsorption of individual bases, which make a debated issue in the context of self-assembly and molecular electronics with a variety of molecular components. MD simulations of a DNA oligomer on a substrate are feasible for several different sequences. The results of such simulations performed with the new classical force field can in turn promote the setup of large-scale docking simulations [32]. Docking simulations are able to reveal a plethora of viable docking geometries, which can eventually be tested and refined by MD and DFT. This repeating cycle will eventually allow us to unravel the conformation of DNA molecules on an inorganic substrate.
To start this ambitious plan, we have selected the Au(111) surface as the substrate, because it is experimentally interesting and already well characterized for MD simulations. To derive the classical force field for DNA/Au(111) MD simulations, it is necessary to perform DFT calculations of each individual base (cytosine, guanine, thymine and adenine) on Au(111). Here we present our DFT results of the cytosine/Au(111) system as a prototype, to demonstrate the two-fold predictive power of this approach: (1) to gain insights in the electronic structure of the system itself; (2) to develop tools (namely, force field parameters) that enable the simulation of more complex systems. We discuss the microscopic nature of the interaction between cytosine and the Au(111) surface. We particularly focus on quantifying the importance of dispersion interactions in order to develop a reliable multi-step method [32].
We investigated cytosine on Au(111) including the van der Waals (vdW) interaction, which was not done in previous studies of the same system [33]. We could do so by benefiting of a recent implementation of a vdW-corrected functional for DFT calculations, named vdW-DF [34, 35]. Indeed, we reveal significant differences comparing the results obtained with and without vdW interaction, both in total energy values and in equilibrium geometries. Our vdW-DF results are in good agreement with experimental data, while DFT results without vdW terms are affected by larger deviations. These results have implications for monolayer formation and contradict a common opinion that the surface-molecule interaction gives only a minor contribution to the monolayer formation energy. In fact, authors have usually neglected the interaction of each base with the surface when dealing with supramolecular structures [36]. Our work, instead, reveals that, even if vdW terms are essential to attain a correct quantitative and qualitative description, the interaction mechanism goes well beyond pure vdW coupling.
2.2. The Method
We performed gradient corrected DFT calculations of cytosine in the gas phase and adsorbed at the Au(111) with the quantum-espresso package [37] (version 4.3), using the PBE exchange correlation functional [38] and the vdW-DF functional [35, 39]. We chose a plane wave basis set with a cutoff of 25 Ry and we described the electron-ion interaction with ultrasoft pseudo-potentials [40]. The surface was modeled with a slab of four Au layers with a periodically repeated 6 × 3√3 surface supercell that contains 36 atoms per layer. The lateral distance between two neighboring cytosine replicas was at least 11 Å and the vacuum thickness in the direction perpendicular to the surface was at least 14 Å, enough neglect the interaction between periodic replicas of the system. The Brillouin zone (BZ) sums were calculated including two Monkhorst–Pack special k points in the irreducible wedge. All the atomic coordinates were relaxed until the forces vanished within 0.05 eV/ Å. Preliminary calculations on benchmark systems allowed us to assess the reliability of the method [15].
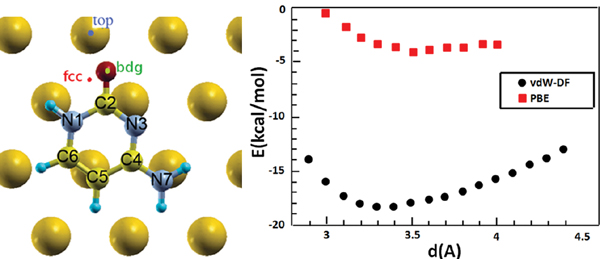
Figure 2 (Left) Top view of a relaxed configuration of cytosine/Au(111). The image defines the atomic labels in the adsorbate and the labels of adsorption sites in the substrate. (Right) Adsorption energy versus cytosine-Au vertical distance (measured between the center of mass of the molecule and the average surface height) for horizontal cytosine on Au(111) at the bdg site. Black and red points denote vdW-DF and DFT [33, 42] results, respectively.
Atomic charges and the amount of charge transfer were evaluated through Løwdin’s population analysis [41].
In the following, we denote with the PBE/vdW-DF (PBE/PBE) label calculations that were done with the PBE functional in the pseudopotential generation and vdW-DF (PBE) functional in the self-consistent runs for the interface. For tests of this ansatz we refer the reader to our original work [15].
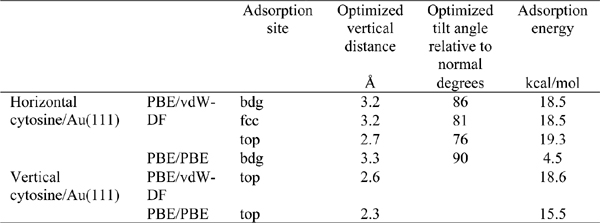
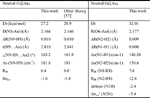
Table 1 Adsorption energies, molecule-surface distances and inclinations for cytosine adsorbed on Au(111) [15]. The adsorption site is the site of the Au(111) triangular lattice on top of which the O2 atom of cytosine resides.
2.3. Structure and Energetics
Different adsorption sites and adsorption geometries were tested for the cytosine/Au(111) interface. We performed vdW-DF calculations for geometry optimization starting from cytosine either parallel (horizontal configurations) or perpendicular (vertical configurations) to the substrate. The O atom of cytosine in the initial conditions was placed above a top (one-fold coordination) bridge (abbreviated bdg, two-fold coordination), or fcc (three-fold coordination) site of the underlying triangular lattice (Figure 2).
We started optimizing the atomic coordinates of the horizontal cytosine/Au(111) system both with and without vdW interactions, starting from an arbitrary configuration with the molecule parallel to the surface at 3.4 Å above Au(111). After the relaxation we performed a series of single-point calculations at frozen internal coordinates by varying the molecule-surface vertical distance. The results are visualized in the plot of Figure 2. The adsorption energy values, which are given by the minima of the curves, are sensibly different in vdW-DF and PBE calculations. PBE calculations give a very shallow minimum, while vdW-DF results produce a deeper minimum at the distance of 3.3 Å, which is more compliant with a variety of results on aromatic systems and heterocycles [43, 44]. Our vdW-DF results are in good agreement with experimental data that report adsorption energy gains between 25 and 36 kcal/mol in the high-coverage regime, while PBE calculations deviate from the ones in [42]. The results are summarized in Table 1.
First of all we note that the adsorption energies for cytosine adsorbed in a horizontal mode at different lattice sites differ by less than 1 kcal/mol, namely they can be considered as degenerate. This qualitative feature also results from calculations without the vdW interaction [45]. It also emerges from AFM results on monolayers, both of cytosine and of other DNA bases, which show that the geometry of the monolayer is not influenced by the geometry of the Au(111) lattice [36].
Furthermore, we point out that in PBE results the vertical configuration is definitely preferred with respect to the horizontal one, while with the vdWDF functional the two configurations have very close adsorption energies and the horizontal one is slightly preferred. This result is in agreement with experimental results that show that cytosine is not able to create a self-assembled monolayer on, e.g., Au(111). Instead, at low coverage cytosine prefers filament structures with a high mobility [36]. In these structures cytosine molecules are always adsorbed horizontally. It is true that the interaction with the other molecules in the filament determine the preferred orientation, but it is also true that, in the presence of a strong preference for a vertical configuration, as for cytosine on Cu(110), monolayers are formed by vertical molecules [36].
The final vdW-DF adsorption energy value of cytosine on Au(111), both in parallel and vertical configurations, gives a remarkable evidence of adsorbate-substrate interaction beyond the pure dispersion regime, despite the fact that dispersion interactions are crucial for a correct description of the system. Another evidence of the interaction between cytosine and Au(111) is the fact that in vdW-DF horizontal configuration results the molecule is tilted respect to the surface and the O atom gets close to the surface. C2-O8 bonding is stretched and the cytosine molecule gains 0.2 e−. Thus, our results indicate that electron transfer occurs from the surface to the adsorbate. We believe that the inclusion of dispersion interactions in the theoretical description is crucial to resolve these subtle effects. More insights on the interface coupling are gained by inspecting the electronic structure, which is presented in the next subsection.
2.4. The Electronic Structure and Binding Mechanisms
To understand what kind of interaction is established between the molecule and the surface, we analyzed the density of states (DOS) and the isosurface plots of electron wavefunctions, according to an established protocol [46].
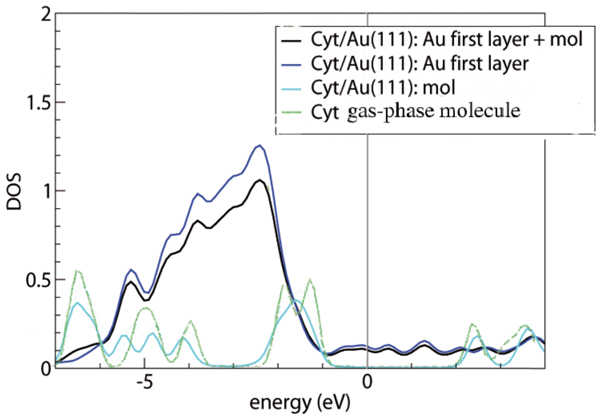
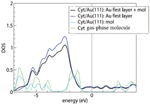
Figure 3 Density of states for cytosine adsorbed on the Au(111) surface, computed by vdWDF. The Fermi level is set at the origin of the energy scale. The deepest energy level, which is the same for the gas-phase molecule and for the adsorbed system, is used for alignment of the various curves. The green line is the DOS of the gas-phase molecule. The cyan, blue and black lines represent the projections of the total cytosine/Au(111) DOS on cytosine, the top Au layer and the sum of cytosine with the top Au layer, respectively, as indicated in the legend. The projected DOS is computed by projecting the total DOS onto atomic orbitals and then summing over all the projections that constitute the subsystems of interest [15]. Reprinted from [15] with permission; © 2012 American Chemical Society.
Figure 3 illustrates the DOS plots from our vdW-DF calculations of gas-phase and adsorbed cytosine. The green curve is the total DOS of the gas-phase molecule. The other curves are projections of the total DOS of the interface system (the most favorable configuration) o various portions of the compound, as detailed in the figure caption and legend. By comparing the green and cyan lines, we can see only minor perturbations on cytosine in going from the gas phase to the adsorbed phase. In particular, around the upper edge of the Au d bands, namely between 2 and 1 eV below the Fermi level, the DOS shows a redistribution of the cytosine peaks. Since the short distance between the O2 atom and Au(111), together with the tilted geometry of the molecule, suggest an interaction stronger than pure dispersion, we inspected the energy ranges where both Au and the molecule have a non negligible DOS to search for hybrid orbitals and possibly bonding orbitals.
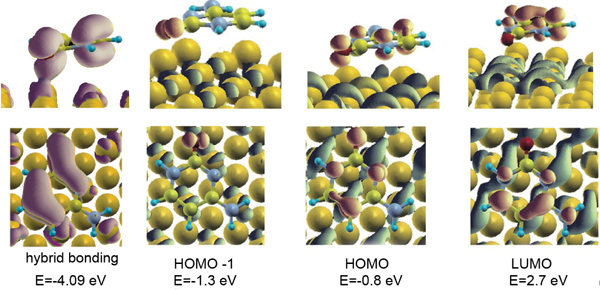
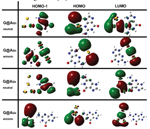
Figure 4 shows isosurface plots of relevant orbitals of the cytosine/Au(111) interface. The systematic analysis of all the single-particle electron wave functions (we visualized many more orbitals than those reported here) reveals the formation of bonding orbitals, of which the leftmost panel in Figure 4 encloses just an illustrative example.
Figure 4 Isosurface plots of representative hybridized orbitals of cytosine adsorbed on Au(111) at the bridge site of the triangular substrate lattice. The leftmost panel shows an example of a bonding orbital between cytosine and the host surface, with a pink isosurface. The other panels show examples of hybrid, but not bonding, orbitals formed with the Au surface by the HOMO-1, HOMO and LUMO: the isosurface portion localized on the surface is blue, the isosurface portion localized on the molecule is red [15]. Reprinted from [15] with permission; © 2012 American Chemical Society.
The Newns–Anderson model for atomic and molecular chemisorption on metal surfaces predicts that the interaction between the localized molecular orbitals and the narrow d band of the metal produces hybrid orbitals of both bonding and antibonding type [47]. This mechanism is found, e.g., in thiols chemisorbed on Au(111) [48] and was accurately discussed in the case of cysteine/Au(111) [46]. The case of the cytosine/Au(111) interface does not comply with the Newn–Anderson picture. We reveal the formation of bonding orbitals but there is not the formation of bonding-antibonding couples from the same molecular orbital and the shift in energy of the bonding orbital respect to the gas-phase molecule is less than 0.5 eV. Only in the energy range of the Au d bands, where molecular orbitals have a component on O2 or N3 atoms, the interaction is strong enough to allow charge sharing and the formation of bonding orbitals.
Our findings point out a kind of interaction that is stronger than pure physisorption and that causes the formation of hybrid orbitals between the molecule and the surface. The analysis of vdW-DF results shows that the interaction between cytosine and Au(111) is beyond the pure dispersion regime, even if dispersion interactions are fundamental to bring the molecule close enough to the surface to exploit the short range interaction between O2, N3 and Au. This interaction is then responsible of the tilted geometry of the horizontal molecule and of the formation of bonding orbitals. This evidence, along with results accumulating from recent works [49–52], contradicts the common belief that homo- and hetero-cycles adsorb on metal surfaces by solely dispersion interactions.
2.5. Future Developments
Similar calculations as those presented above have been carried out for all the bases. They allowed us to develop a preliminary DFT based force-field for classical molecular dynamics simulations of DNA on Au(111): this force field is in the final phase of testing before release. The next release of the force-field will include a refinement to take into account the interaction of the sugar-phosphate backbone with the substrate: we expect this correction to be minor, because of weak coupling. In the long term, we plan to proceed along the conceptual strategy outlined in Section 2.1.
3. The Interaction of DNA Bases with Nanostructured Gold: The Case of Guanine at Small Au Clusters
3.1. Motivation and Background
In various investigations of DNA and peptides on Au(111), we recently noticed an unexpected degree of electronic coupling. For example, the dative-bond between a hydroxyl-rich beta-sheet and a gold surface is the essential component of the recognition mechanism [53]. Furthermore, we revealed (section 1.2) electronic hybridization at the cytosine/Au(111) interface [15]. Experimental methods have confirmed that in low coverage DNA strain could wrap the gold nanoparticles [54–56]. It is well known that the adsorption of biomolecules on gold surface/nanoparticles is actually a dynamic process, which depends on the details of adsorbate nature, molecule coverage and environment. DNA bases can adsorb on nanoparticles in various configurations such as parallel and tilted and employing different molecular atoms/groups, depending on the potential energy surface. Here we focus on the formation of unusual H-bonding between guanine (G) and size-expanded guanine (xG) with gold clusters, as a model of the situation at the edges of nanoparticles.
In 2005, Kryachko and Remale investigated the interaction between guanine and small gold clusters by DFT [57]. They determined that the bonding occurs via the N and O atoms in the base and one gold atom. They also showed that this chemical bonding could be reinforced by NH···Au unconventional hydrogen bonds nearby. After that, there were several reports about the unconventional hydrogen bonds in the gold based complexes. Shukla and coworkers investigated the interaction of the guanine base and the Watson– Crick guanine-cytosine base pair with larger gold clusters Aun (n = 2, 4, 6, 8, 10, and 12): their results confirmed the bonding between N and Au atoms [58]. Other groups investigated the interaction between DNA bases [59] or base pairs with the Au20 cluster [60]. Recently, Cao and coworkers studied the nucleobase-gold complexes with anion photoelectron spectroscopy and DFT calculations and confirmed the existence of NH···Au hydrogen bonds through experimental measurements [61]. In all the past studies, the authors characterized the binding sites and electron affinity/ionization processes, while mostly omitting information on the detailed topology of the NH···Au hydrogen bonding and N/O-Au bonding. Some questions naturally arise: What is the nature of these interactions? How do the unconventional hydrogen bonds influence the geometrical and electronic properties of these complexes? Is there a way to tune these special interactions? We believe that answering these questions is relevant to explore biomolecule-gold surface/nanoparticle interactions, especially at the edge of nanoparticles and at irregular surfaces. Very recently, it was determined that gold clusters (Au18 and Au27) tend to pump electrons to the corner and edge sites, making these sites more electronically active than surface sites [62]. Accordingly, the different electronic reactivity of gold atoms at surface, corner or edge sites of nanoparticles may significantly influence the binding orientation of nucleobases on them and consequently the electronic properties of the resulting systems. All these phenomena and questions motivated us to get the insights into these special interactions. A guanine molecule in complex with a Au3/Au4 cluster are employed to construct atomic models to investigate this problem. We choose guanine among the DNA bases because, due to its low ionization potential (IP) compared with adenine, thymine and cytosine, is expected to play a major role in DNA conductance and lesion/damage processes. Au3 and Au4 represent two typical gold clusters, odd and even. It is well known that there is an odd-even effect for the binding strength in gold clusters.
Based on previous work by Kryachko [57], Shukla [58], Cao [61] and others [59, 60], we deduced an initial scheme for the adsorption process of guanine on a gold substrate: on one hand, π-π stacking between molecule and substrate in a horizontal relative orientation would lead to stability by maximizing orbital mixing; on the other hand, direct N/O-Au bonding between molecule and substrate, possibly reinforced by unconventional NH···Au hydrogen bonds, would play a crucial role in an inclined relative orientation for some special conditions. The goal of our work presented in this section is to understand the nature of G@Au3/Au4 coupling and explore ways to tune the competition between horizontal and inclined orientations. The label G@Aun (xG@Aun) indicates the complex between G (xG) and the Aun cluster.
In addition to the G base, we also conside xG. In the past ten years, interest in the use of modified analogs of DNA as templates for growing nano-particle complexes has increased significantly, aiming to reveal whether these new alternative genetic systems could exist for therapeutic and biotechnological applications. Experimental investigations demonstrated the feasibility and stability of DNA double helices that contain size-expanded base pairs [22, 63]. Theoretical studies have shown that the xDNA bases have more electron conjugation than the natural bases in the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), which in turn affects the value of HOMO-LUMO gap [24, 64–66]. The greater -conjugation may induce strong π-π coupling between stacked bases and bases pairs, for easier charge transfer [23]. Sharma et al. utilized a DFT method to investigate the interaction between x-bases (xA, xC, xT and xG) and the Au6 cluster with the aim of inquiring on the possibility of enhancing conductivity in size-expanded nucleic acids tagged by gold atoms [67]. Bu’s group carried out some work on the rational design of hetero-ring-expanded DNA base analogs and determined that the x-bases may be considered as DNA genetic motifs and serve as building blocks in the development of molecular electronic devices [68, 69]. We take steps from these existing data for a deeper investigation of the bonding topology. We wish to understand if and how chemical modifications of the bases affect the DNA@Au binding and in particular the unconventional H-bonding. Progress in this field will offer more information on the potential molecular wire application of natural and modified DNAs.
3.2. The Method
Geometry optimizations have been done with the B3LYP exchange-correlation functional [70] in its restricted and unrestricted forms, employing the LANL2DZ and 6-31+G* basis sets for Au and the natural guanine/xguanine, respectively. Frequency calculations at the same level were performed as well, to ensure that the equilibrium systems represent true minima on the potential energy surfaces. No symmetry constraint was imposed during the geometry optimizations. The basis set superposition error (BSSE) was corrected by using the counterpoise procedure of Boys and Bernardi [71]. The natural bond orbital (NBO) analysis of charge population and other electronic properties were studied at the B3LYP/LANL2DZU 6-311++G** level. All calculations have been performed with the Gaussian03 suite of codes. Topological properties of the electron density at the bond critical points (BCPs) of the NH···Au and OH···Au hydrogen bonds were characterized using the Atoms in Molecules (AIM) methodology [72] at the B3LYP/LANL2DZU 6-311++G** level.
To analyze and visualize the non-covalent interaction in these systems, the non-covalent interaction index (NCI) approach, developed by Yang et al. [73], was adopted. The Multiwfn software [74] was used to calculate relevant quantities of this approach. More details are reported elsewhere [16].
3.3. Structure and Energetics
3.3.1. Natural Guanine
Our initial neutral G@Au3/Au4 structures were taken from the most stable geometries described by Kryachko and Remacle [57]. Our optimized structures of the neutral G@Au3 and G@Au4 complexes at B3LYP/LANL2DZU 6-31+G* level are shown in Figure 5. Tests at the MP2/LANL2DZU 6-31+G* level assessed the accuracy of the B3LYP/LANL2DZU 6-31+G* results.
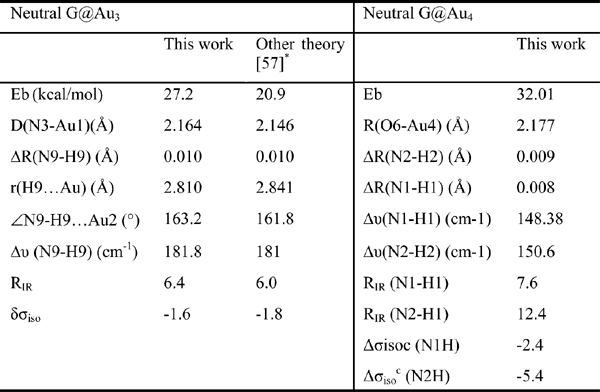
In Table 2 we present the some key features of neutral G@Au3 and G@Au4 systems computed by us. We find the length of the N3-Au bond to be 2.164 Å, which is only 0.018 Å longer than in previous work. This tiny difference stems from the different basis sets for treating gold atoms and is not significant. The results reported in Table 2 overall demonstrate a good agreement with the previous theoretical data. According to six criteria to justify hydrogen bond formation, vdW cutoff, red shift of infrared intensity (RIR) and downfield shift of nuclear magnetic resonance (σiso), Kryachko and Remacle found out that the unconventional NH···Au bonds obey all the necessary prerequisites of standard H bonds [57]. On the basis of our results in Table 2, we draw the same conclusion.
In order to assess the bonding energy between nitrogen and gold atoms in the G@Au3 neutral complex, we artificially constrained the complex to a different geometry. Specifically, we rotated the Au3 cluster so that the Au3 triangle becomes perpendicular to the guanine plane, without changing the internal geometry of the cluster and the guanine, nor the N3-Au1 distance. After this step, the N9H···Au3 bond is broken while the N3-Au1 bond is kept. The BSSE corrected binding energy is 21.35 kcal/mol for this geometry, so the N9H···Au3 bonding energy is approximately 5.85 kcal/mol. Since the BSSE corrected binding energy for the G-C base pair at the B3LYP/6-311++G**//B3LYP/6-31+G* is 28.4 kcal/mol, the average contribution of each of the three hydrogen bonds in the G-C pair is about 9.5 kcal/mol. Hence, we find that the unconventional hydrogen bond in the neutral G@Au3 complex is weaker than that in a Watson–Crick H-bond in the GC pair.
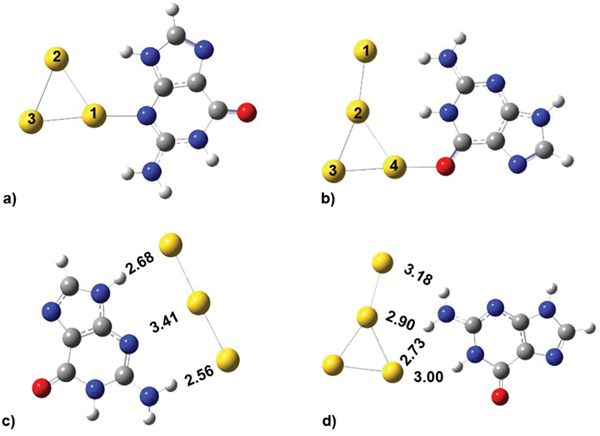
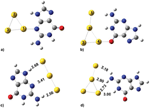
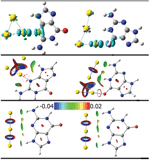
Figure 5 The stable structures for neutral G@Au3 (a), G@Au4 (b), and anionic G@Au−3(c), G@Au−4(d) complexes.
Due to their large electron affinity, small gold clusters would like to accept an excess electron to be in a more stable anionic state [75]. We want to explore whether the excess electron would increase or decrease the binding strength between gold clusters and the guanine molecule and modify the process of charge transfer in the system.
We optimized the atomic coordinates of the negatively charged G@Au−3 and G@Au−4 complexes starting from the equilibrium structures of the corresponding neutral complexes, with one net negative charge added to each system. The optimization process was implemented at the B3LYP/LANL2DZU 6-31+G* level as used in the neutral complexes. The BSSE corrected binding energy is 14.24 and 15.37 kcal/mol for the G@Au−3 and G@Au−4 complex, respectively. These values are about 50% smaller than those found for the neutral complexes. It indicates that the excess electron decreases the binding strength, in agreement with previous indications for different nucleobases. The optimized geometries are presented in Figures 5(c,d), with indication of all the distances between gold atoms and the neighboring hydrogen and nitrogen atoms. In the G@Au−3 complex the shape of the gold cluster changes from triangular to linear: The angle between the three gold atoms is 178.5°. The N3-Au1 distance increases significantly as compared to neutral G@Au3, by about 1.25 Å. The N9H···Au2 distance increases by 0.2 Å and anotherN2H···Au3 hydrogen bond forms. To determine the binding energy of the elongated N3-Au1 bond, we adopted the same procedure as described for the neutral complexes, namely rotating the gold rod 90°, while keeping the coordinates of guanine and of the Au1 atom fixed. Thus, the gold rod becomes perpendicular to the guanine plane and the H-bonds are broken. The BSSE corrected binding energy for this structure is 9.56 kcal/mol, which is significantly smaller than its counterpart in neutral complex (21.53 kcal/mol). Therefore, the elongated N3-Au1 bond in the G@Au−3 complex is weaker by ∼12 kcal/mol than the corresponding bond in the neutral G@Au3 complex. In the G@Au−4 complex, the T-shape of the gold cluster does not change significantly as compared to the G@Au4 neutral system. However, the relative guanine/gold orientation changes. We do not find the O6-Au1 bond in G@Au−4, because the gold cluster slides to the N1 and N2 sites of guanine. Hence, there is only hydrogen bonding in the G@Au−4 cluster, without covalent bonding.
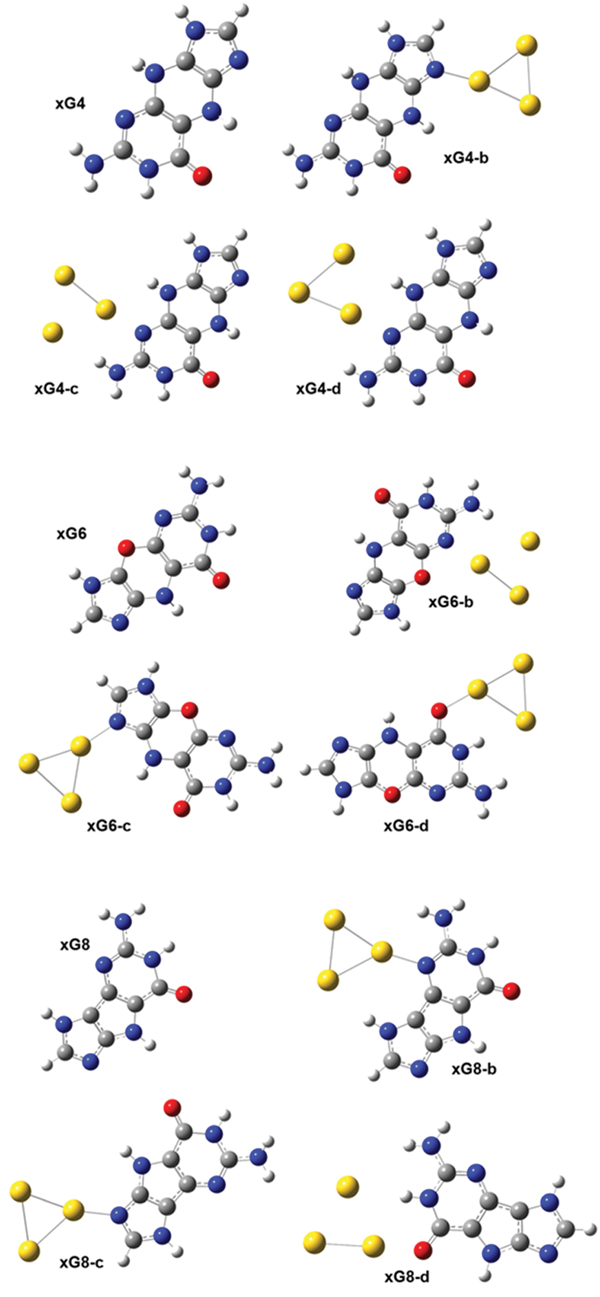
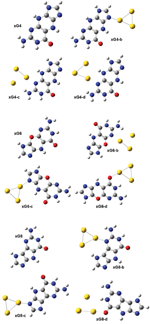
Figure 6 The optimized geometries of the neutral gas-phase xG4, xG6 and xG8 and of the neutral xGn@Au3 complexes (n = 4, 6 and 8).
Table 2 Some key features of neutral G@Au3 and G@Au4 complexes. The binding energy (Eb) includes the BSSE correction. It is computed as the total energy of the complex minus the total energies of the isolated guanine and cluster. RIR is the ratio of the IR activities of the N-H stretching mode involved in H-bond in the complex and in isolated guanine. Δσiso is the NMR shift (in ppm) taken with respect to the isolated guanine and gold cluster.
3.3.2. Size Expanded Guanine
We considered two different forms of xG, characterized by different conjugation in the spacer ring [16]: the structures of xG4, xG6 and xG8 are defined in Figure 6. Three initial structures were designed for the xG4@Au3 complex: the Au3 cluster has a triangular shape; one Au atom binds to either N7 (Figure 2 xG4-b) or N3 (Figure 2 xG4-c and xG4-d). A NH···Au hydrogen bond was designed in all the initial structures. After optimization, we could not achieve a stable isomer with gold attaching to the oxygen atom of xG4. It should be noted that for the complexes in which the gold-molecule contact is through the N3 site of xG4 (Figure 2, xG4-c,d), the initial geometries are essentially maintained, including the presence of the NH···Au hydrogen bond. However, for the complex in which the gold-molecule contact is through the N7 site of xG4, after optimization the NH···Au hydrogen bond is broken.
Among the three xG4@Au3 isomers, xG4-b has the lowest total energy, which could be partly explained by the torsion of the xG4 molecule. The xG4 molecule in the gas phase is not exactly planar, with a 166.9° folding angle. The folding angles of xG4 in the three xG4@Au3 isomers are 168.9, 169.6 and 173.3°, respectively. The BSSE corrected binding energy for the most stable isomer is 27.90 kcal/mol. The energy difference between isomers xG4-c and xG4-d is negligible within the precision of our approach. The fact that the most stable xG4@Au3 isomer is the one in which the gold-molecule contact is through the N7 site of xG4 and no unconventional hydrogen bond is formed contradicts the expectation that NH···Au hydrogen bonding would reinforce the N/O-Au bond during the combination of cluster and molecule, as we found in the G@Au3 cluster with natural guanine. We infer that this peculiar behavior of xG4 in complex with a small gold cluster is due to the steric effect caused by the spacer ring.
Compared with xG4, one NH is replaced by oxygen in the spacer ring of xG6. Introducing one oxygen atom in the spacer ring could in principle increase the planarity, but in our results the optimized xG6 is still not planar. xG8 has, instead, a five-membered spacer ring, which should also facilitate planarity. It should be noted that xG6 has the second lowest HOMO-LUMO gap in the series of size-expanded guanines. Three stable isomers for each of the xG6@Au3 and xG8@Au3 complexes are shown in Figure 6. The isomer xG6-c is the most favorable among the three xG6@Au3 complexes. The BSSE corrected binding energy is 27.04 kcal/mol, very similar to the binding energy of the lowest-energy xG4@Au3 complex. The binding pattern is also similar, with gold-molecule contact occurring at the N7 site of xG6. The isomer xG8-b is the most favorable among the three xG8@Au3 complexes. The BSSE corrected binding energy is 30.42 kcal/mol, higher than that of xG4@Au3 by 2.52 kcal/mol. In this structure, due to the overall good planarity and a reduced steric hindrance, a NH···Au can be established to reinforce the N-Au covalent bonding. The xG8@Au3 complex has the largest binding strength of all the xGn@Au3 sampled complexes because of the minor molecular torsion, which in turn enables the formation of NH···Au hydrogen bond.
3.4. The Electronic Structure and Binding Mechanisms
3.4.1. Natural Guanine
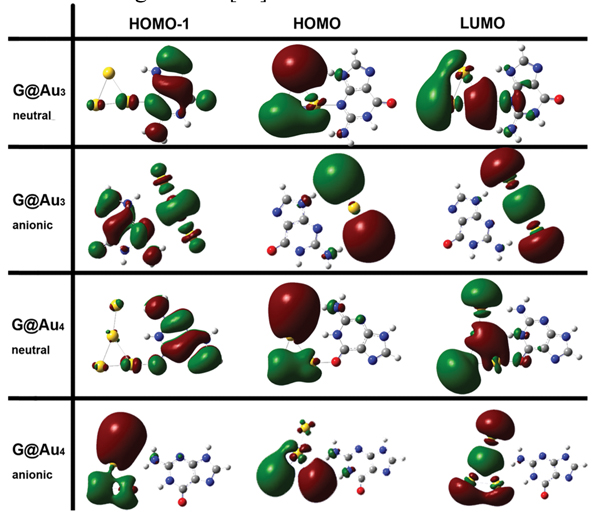
The results of the NBO analysis and the shape of the frontier molecular orbitals (Figure 7) indicate that each anchoring bond (N3-Au in G@Au3 and O6-Au in G@Au4) involves charge transfer from G to Au. Instead, each unconventional hydrogen bond (one in G@Au3, two in G@Au4) is characterized by charge transfer from gold to G [16].
Charge transfers can be visualized through the electron density difference between the associated state and the isolated individual building blocks. This is shown in the top panel of Figure 8. We find that in the neutral G@Au3 complex the charge variation is mostly due to the covalent N3-Au1 bonding, with minor contributions from the hydrogen bonds.
According to the NBO analysis, the amount of charge transfer from the guanine molecule to the gold cluster is −0.117e and −0.073e in G@Au3 and G@Au4, respectively. Namely, during complex formation electrons are transferred from the molecule to the cluster. The amount of electronic charge transferred to the Au3 cluster is larger than that transferred to the Au4 cluster, due to the different anchoring sites. In the G@Au4 complex, the gold cluster anchors to the oxygen atom of guanine, which has larger electronegativity than the nitrogen anchoring site in the G@Au3 complex. Furthermore, the amount of charge transfer has the same trend as the electron affinity (EA) of the Au3 (3.85eV)andAu4 (2.77 eV) clusters. Our result obtained by the NBO method is consistent with the statement found elsewhere that “gold clusters with an odd number of atoms are better electron acceptors and better electron donors than clusters with and even number of atoms” [60].
Figure 7 Isosurface plots (s = 0.02 a.u.) frontier orbitals for the G@Au3 and G@Au4 complexes in neutral and anionic states.
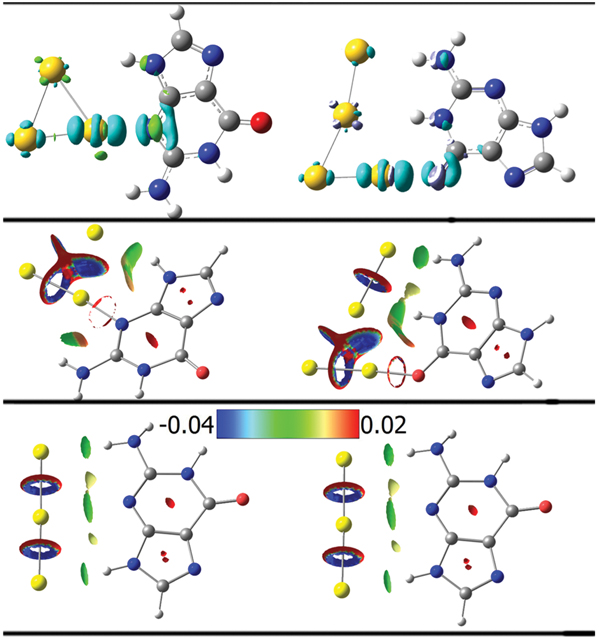
The analysis of the charge density and its Laplacian at the bond critical points (BCP) sheds more light into the nature of the unconventional hydrogen bonds in the complexes. Our results indicate that the (3, −1) BCP exists in the NH···Au hydrogen bonds and in the N/O-Au bonds. It is easy to comprehend that the nature of the NH···Au is a hydrogen bond. What is the nature, however, of the N/O-Au bonds? By analyzing the local energy density E(r), we could determine that the N/O-Au bonds are covalent [16].
It is noteworthy that in the neutral G@Au4 complex, according to the AIM analysis [72], there is no hydrogen bond between N1H and the middle Au2 atom, namely no (3, −1) BCPs. However, according to the same rule we find a hydrogen bond between N1H and the Au4 atom. This is somewhat strange in terms of the atomic distances. In fact, the distance N1H···Au2 in the neutral G@Au4 complex is 2.875 Å, larger than the N1H···Au4 distance in the same complex but comparable to the N9H···Au2 distance in the G@Au3 complex, and the latter contact was found compatible with H-bonding through the AIM analysis. To further explore the nature of the N1H···Au2 contact, we utilized Yang’s approach, according to which one can use the sign of λ2 (the second largest eigenvalue of the electron density Hessian) to distinguish bonded (λ2 < 0) from non-bonded (λ2 > 0) interactions. The results of this analysis are presented in Figure 8, where the gradient isosurfaces are colored according to the corresponding values of sign(λ2)ρ, which is a good indicator of interaction strength. Large negative values of sign(λ2)ρ are indicative of attractive interactions (such as dipole-dipole or hydrogen bonding). Large negative values of sign(λ2)ρ are indicative of non-bonding interactions. Values of sign(λ2)ρ close to zero indicate weak van der Waals interactions. The isosurface plots shown in the middle of Figure 4 indicate the existence of a H-bond between N1HandtheAu2 atom in the neutral G@Au4 complex, which instead does not emerge from the BCP analysis. This is a genuine result of our work, which goes beyond previous descriptions. Essentially, we find that Yang’s approach performs better than AIM theory in treating this system. The blind point of AIM in the description of the G@Au4 complex may arise from the use of pseudopotientials. The analysis of the frontier molecular orbitals (Figure 7) indicates that both HOMO and LUMO in the anionic complexes are localized on the gold cluster moiety, which could be expected on the basis of the large electron affinity of the gold cluster. The NBO charge population analysis shows that the amount of gold-localized charge in the G@Au−3 and G@Au−4 complexes is −0.927e and −0.936e, respectively. Also in this case we find a blind point among the BCPs, which can be corrected through the Yang’s approach [16]. In fact, the bottom panel in Figure 8 shows the existence of a hydrogen bond between N2Hand the Au2 atom in the G@Au−4 anionic complex.
Figure 8 Isosurface plots of the electron density difference (top, s = 0.005 a.u.), the reduced density gradient (middle, s = 0.500 a.u.) for the neutral G@Au3 and G@Au4 complexes and the anionic G@Au−$$$3 and G@Au−$$$4 complexes (bottom, s = 0.500 a.u.). The green and cyan isosurfaces in the top plots identify the regions in which the electron density is increased and decreased, respectively, upon complex formation relative to the independent species. The isosurfaces of the reduced density gradient in the bottom plots are colored according to the values of the quantity sign(λ2)ρ and the RGB scale is indicated.
3.4.2. Size Expanded Guanine
The HOMO-LUMO gap for the three xG4@Au3 isomers (b, c and d) is 2.40, 2.22 and 2.45 eV, respectively, which is slightly smaller than that of the G@Au3 complex (2.46 eV).
Comparing the three types of novel size-expanded guanine molecules, we can draw some interesting conclusions. Although the NH site in the spacer ring may supply a new opportunity for forming NH···Au hydrogen bonds in complexes of size-expanded guanine with small gold clusters, this does not occur, because of significant steric effects that hinder further molecule-gold contacts. The introduction of a spacer ring in guanine is an effective tool to decrease the HOMO-LUMO gap and expand the π-conjugation area. These electronic effects were already discussed by other authors [23, 24, 64, 65]. The new characteristic that we find in our work, namely the enhanced steric hindrance, may have other appealing consequences for surface-immobilized DNA-based devices. In fact, our results indicate that the size-expanded guanine molecule favors an adsorption orientation on gold that conduces to π-π stacking, rather than a configuration that maximizes the number of point contacts. The size-expanded design would make the adsorption or assembly process between DNA bases and gold surface/nanoparticle more orderly. As a consequence of all these evidences, we suggest that the new designed size-expanded guanine molecules should have an optimal performance in DNA-based devices because of (1) the good inherent charge transfer capabilities imparted by the low HOMO-LUMO gap and large -conjugation area [23] and (2) the highly uniform adsorption orientation caused by the enhanced steric hindrance [16]. The latter issue deserves further attention and is the object of ongoing studies. It means that not only the inherent molecular properties are important to develop molecular devices, but also the interaction of the molecules with the inorganic components. Both aspects can be exploited to improve the current state-of-the-art.
3.5. Perspectives
The natural continuation of this work is the investigation of more and more bonding schemes between guanine bases and gold substrates. In particular, we are now focusing on thiol bonds realized by attaching different thiol linkers to a guanine base that is thought as a possible termination of a DNA molecule. Our goal is to identify effects of the chemistry and length of the linker in charge transfer from the substrate (electrode) to the DNA chain.
4. Summary and Outlook
In this article we surveyed our recent work devoted to interfaces between DNA and metal substrates. The substrates that we have in mind can be perfect or defected two-dimensional surfaces, as well as finite-size nanoparticles.
We have revealed important effects of electronic hybridization between nucleobases and Au, similar to the adsorption mechanisms of other homo-and hetero-cycles on Au. Furthermore, we have pointed out that also hydrogen bonding between adsorbate and substrate can be relevant at edges or defects. We have also found that aromatic size-expansion improves not only the electronic structure of the guanine base in view of charge transfer, but also the surface adhesion, which is an additional motivation for its appeal in nanotechnology, besides its obvious impact in biochemistry and molecular biology.
Although we investigated the adsorption of individual bases and not entire DNA oligomers, these results pose the foundations to tackle the more complex interfaces of technological interest.
Before reaching the capability of investigating entire DNA molecules on a surface or a nanoparticle, our short-term interest in the evolutionary line of this work concentrates on developing an AMBER-like force field to enable classical MD simulations of DNA on Au(111) and on probing surface-molecule charge transfer at guanine/Au(111) interfaces realized with different thiol bonding motifs.
Acknowledgements
This work was funded by the European Commission through project “DNANanodevices” (Contract #FP6-029192), by the ESF through the COST Action MP0802, by the Italian Institute of Technology through project MOPROSURF and the Computational Platform, by Fondazione Cassa di Risparmio di Modena through Progetto Internazionalizzazione 2011. The ISCRA staff at CINECA (Bologna, Italy) is acknowledged for computational facilities and technical support.
References
[1] E. Braun, et al. Nature, 391(6669),775–778 (1998).
[2] P. J. de Pablo, et al. Physical Review Letters, 85(23), 4992–4995 (2000).
[3] H. W. Fink, C. Schonenberger Nature, 398(6726), 407–410 (1999).
[4] D. Porath, et al. Nature, 403(6770), 635–638 (2000).
[5] R. G. Endres, D. L. Cox, R. R. P. Singh Reviews of Modern Physics, 76(1), 195–214 (2004).
[6] D. Porath, G. Cuniberti, R. Di Felice Long-Range Charge Transfer in DNA Ii, 237, 183–227 (2004).
[7] H. Cohen, et al. Proceedings of the National Academy of Sciences of the United States of America, 102(33), 11589–11593 (2005).
[8] B. Xu, et al. Nano Letters, 4(6), 1105–1108 (2004).
[9] M. Zwolak, M. Di Ventra Reviews of Modern Physics, 80(1), 141–165 (2008).
[10] H. Cohen, et al. Nano Letters, 7(4), 981–986 (2007).
[11] D. A. Ryndyk, et al. Acs Nano, 3(7), 1651–1656 (2009).
[12] E. Shapir, et al. Advanced Materials, 23(37), 4290–4294 (2011).
[13] E. Shapir, et al. Nature Materials, 7(1), 68–74 (2008).
[14] E. Shapir, et al. Journal of Physical Chemistry C, 114(50), 22079–22084 (2010).
[15] M. Rosa, S. Corni, R. Di Felice Journal of Physical Chemistry C, 116(40), 21366–21373 (2012).
[16] W. Sun, R. Di Felice Journal of Physical Chemistry C, 116(47), 24954–24961 (2012).
[17] R. Di Felice, et al. Physical Review B, 65(4) (2002).
[18] A. Calzolari, et al. Applied Physics Letters, 80(18), 3331–3333 (2002).
[19] R. Di Felice, et al. Journal of Physical Chemistry B, 109(47), 22301–22307 (2005).
[20] P. B. Woiczikowski, et al. Journal of Chemical Physics, 133(3), Art No. 035103 (2010).
[21] G. Brancolini, R. Di Felice Journal of Physical Chemistry B, 112(45), 14281–14290 (2008).
[22] A. T. Krueger, et al. Accounts of Chemical Research, 40(2), 141–150 (2007).
[23] A. Migliore, et al. Journal of Physical Chemistry B, 113(28), 9402–9415 (2009).
[24] D. Varsano, A. Garbesi, R. Di Felice Journal of Physical Chemistry B, 111(50), 14012– 14021 (2007).
[25] A. Troisi, G. Orlandi Journal of Physical Chemistry B, 106(8), 2093–2101 (2002).
[26] R. Gutierrez, et al. New Journal of Physics, 12, Art No. 208102 (2010).
[27] P. B. Woiczikowski, et al. Journal of Chemical Physics, 130(21), Art. No. 215104 (2009).
[28] R. Gutierrez, et al. Physical Review Letters, 102(20), Art. No. 208102 (2009).
[29] T. Ghane, et al. Journal of Physical Chemistry B, 116(35), 10693–10702 (2012).
[30] M. H. Lee, et al. Journal of Physical Chemistry B, 116(36), 10977–10985 (2012).
[31] S. S. Mallajosyula, S. K. Pati Journal of Physical Chemistry Letters, 1(12), 1881–1894 (2010).
[32] R. Di Felice, S. Corni Journal of Physical Chemistry Letters, 2(13), 1510–1519 (2011).
[33] S. Piana, A. Bilic Journal of Physical Chemistry B, 110(46), 23467–23471 (2006).
[34] D. C. Langreth, et al. International Journal of Quantum Chemistry, 101(5), 599–610 (2005).
[35] T. Thonhauser, et al. Physical Review B, 76(12), Art. No. 125112 (2007).
[36] R. E. A. Kelly, et al. Journal of Chemical Physics, 129(18), Art. No. 184707 (2008).
[37] P. Giannozzi, et al. Journal of Physics-Condensed Matter, 21(39), Art. No. 395502 (2009).
[38] J. P. Perdew, K. Burke, M. Ernzerhof Physical Review Letters, 77(18), 3865–3868 (1996).
[39] M. Dion, et al. Physical Review Letters, 92(24), Art. No. 246401 (2004).
[40] D. Vanderbilt Physical Review B, 41(11), 7892–7895 (1990).
[41] P. O. Lowdin Journal of Chemical Physics, 18(3), 365–375 (1950).
[42] M. Ostblom, et al. Journal of Physical Chemistry B, 109(31), 15150–15160 (2005).
[43] S. K. M. Henze, et al. Surface Science, 601(6), 1566–1573 (2007).
[44] F. S. Tautz Progress in Surface Science, 82(9–12), 479–520 (2007).
[45] S. Rapino, F. Zerbetto Langmuir, 21(6), 2512–2518 (2005).
[46] R. Di Felice, A. Selloni, E. Molinari Journal of Physical Chemistry B, 107(5), 1151– 1156 (2003).
[47] B. Hammer, J. K. Norskov Chemisorption and Reactivity on Supported Clusters and Thin Films, 331, 285–351 (1997).
[48] M. C. Vargas, et al. Journal of Physical Chemistry B, 105(39), 9509–9513 (2001).
[49] A. Ferretti, et al. Physical Review Letters, 99(4), Art. No. 046802 (2007).
[50] F. Iori, S. Corni, R. Di Felice Journal of Physical Chemistry C, 112(35), 13540–13545 (2008).
[51] N. Lorente, et al. Physical Review B, 68(15), Art. No. 155401 (2003).
[52] K. Toyoda, et al. Journal of Chemical Physics, 132(13), Art. No. 134703 (2010).
[53] A. Calzolari, et al. Journal of the American Chemical Society, 132(13), 4790–4795 (2010).
[54] I. Lynch, A. Salvati, K. A. Dawson Nature Nanotechnology, 4(9), 546–547 (2009).
[55] J. J. Storhofff, et al. Langmuir, 18(17), 6666–6670 (2002).
[56] C. Tamerler, M. Sarikaya Philosophical Transactions of the Royal Society a-Mathematical Physical and Engineering Sciences, 367(1894), 1705–1726 (2009).
[57] E. S. Kryachko, F. Remacle Nano Letters, 5(4), 735–739 (2005).
[58] M. K. Shukla, et al. Journal of Physical Chemistry C, 113(10), 3960–3966 (2009).
[59] A. Kumar, P. C. Mishra, S. Suhai Journal of Physical Chemistry A, 110(24), 7719–7727 (2006).
[60] A. Martinez Journal of Physical Chemistry C, 114(49), 21240–21246 (2010).
[61] G. J. Cao, et al. Journal of Chemical Physics, 136(1), Art. No. 014305 (2012).
[62] A. Moghaddasi, M. Zahedi, P. Watson Journal of Physical Chemistry C, 116(8), 5014– 5018 (2012).
[63] H. B. Liu, et al. Science, 302(5646), 868–871 (2003).
[64] M. Fuentes–Cabrera, et al. Journal of Physical Chemistry B, 110(12), 6379–6384 (2006).
[65] M. Fuentes–Cabrera, B. G. Sumpter, J. C. Wells Journal of Physical Chemistry B, 109(44), 21135–21139 (2005).
[66] A. M. Leconte, F. E. Romesberg Nature, 444(7119), 553 (2006).
[67] P. Sharma, et al. Journal of Chemical Theory and Computation, 3(6), 2301–2311 (2007).
[68] L. Han, et al. Journal of Physical Chemistry B, 113(13), 4407–4412 (2009).
[69] J. M. Zhang, R. I. Cukier, Y. X. Bu Journal of Physical Chemistry B, 111(28), 8335– 8341 (2007).
[70] C. T. Lee, W. T. Yang, R. G. Parr Physical Review B, 37(2), 785–789 (1988).
[71] S. F. Boys, F. Bernardi Molecular Physics, 19(4), 553 (1970).
[72] R. F. W. Bader Chemical Reviews, 91(5), 893–928 (1991).
[73] E. R. Johnson, et al. Journal of the American Chemical Society, 132(18), 6498–6506 (2010).
[74] T. Lu, F. W. Chen Journal of Computational Chemistry, 33(5), 580–592 (2012).
[75] A. Martinez Journal of Physical Chemistry A, 113(6), 1134–1140 (2009).
Biographies

Marta Rosa studied Physics in Bologna, Italy, where she received her Laurea in 2010. She is currently a PhD student in Physics in Modena, Italy. Her PhD research program focuses on understanding the mechanisms of formation of complexes between DNA molecules and extended Au surfaces with a multi-step computational approach that ranges from ab initio to empirical docking.

Wenming Sun was born in Feicheng, China, January 1985. He received his B.Sc degree in Chemistry from Shandong University, China. He obtained his Ph.D. in Theoretical and Computational Chemistry, under supervision of Prof. Yuxiang Bu, from Shandong University. He joined Rosa Di Felice’s group, as a post-doc at the Center S3, CNR Institute of Nanoscience (Modena, Italy) in November 2011. His research activity is mostly in the field of charge transfer at biomolecule-inorganic interfaces.

Rosa Di Felice received her Ph.D. in Physics in 1996 at the University of Rome “Tor Vergata”, Italy. She is a member of the research staff in the Italian National Research Council (CNR, previously INFM) in Modena, Italy, since 2001. She is an author of about 100 peer reviewed journal papers. Her current research interests focus on the theoretical/computational investigation of the electronic structure of nucleic acids and surfaces and of their complexes with inorganic materials.